搜索
【题目】如图，二次函数
的图象与y轴正半轴相交，其顶点坐标为（
，1），下列结论：①abc＞0；②a=b；③a=4c﹣4；④方程
有两个相等的实数根，其中正确的结论是______．（只填序号即可）．
参考答案：
【答案】③④．
【解析】解：①∵根据图示知，抛物线开口方向向下，∴a＜0．
由对称轴在y轴的右侧知b＞0，∵抛物线与y轴正半轴相交，∴c＞0，∴abc＜0．故①错误；
②∵抛物线的对称轴直线x=
，∴a=﹣b．故②错误；
③∵该抛物线的顶点坐标为（
，1），∴1=
，∴b2﹣4ac=﹣4a．∵b=﹣a，∴a2﹣4ac=﹣4a，∵a≠0，等式两边除以a，得a﹣4c=﹣4，即a=4c﹣4．故③正确；
④∵二次函数
的最大值为1，即
，∴方程
有两个相等的实数根．故④正确．
综上所述，正确的结论有③④．
故答案为：③④．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程
（1）﹣3x﹣5=23+2x
（2）3x﹣7（x﹣1）=2﹣3（x+3）
（3）
（4）
-
科目： 来源： 题型：
查看答案和解析>>【题目】18世纪最杰出的瑞士数学家欧拉，最先把关于x的多项式用符号“f（x）”表示，如f（x）＝﹣3x2+2x﹣1，把x＝﹣2时多项式的值表示为f（﹣2），则f（﹣2）＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”，一般地，把
记作
，读作“a的圈n次方” 请你阅读以上材料并完成下列问题：
（1）直接写出计算结果：3⑧= ，
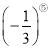= ． （2）我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？仔细思考，将下列运算结果直接写成幂的形式．5⑦= ；（﹣2）⑩= ；（﹣
）⑨= ．（3）计算：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB＝90°，直角边AO在x轴上，且AO＝1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O＝2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O＝2A1O……依此规律，得到等腰直角三角形A2 017OB2 017．则点B2 017的坐标（ ）
A. （22 017，－22 017） B. （22 016，－22 016） C. （22 017，22 017） D. （22 016，22 016）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△OA0A1在平面直角坐标系内，∠OA0A1=90°，∠A0OA1=30°，以OA1为直角边向外作Rt△OA1A2，使∠OA1A2=90°，∠A1OA2=30°，以OA2为直角边向外作Rt△OA2A3，使∠OA2A3=90°，∠A2OA3=30°，按此方法进行下去，得到Rt△OA3A4，Rt△OA4A5，…，Rt△OA2016A2017，若点A0（1，0），则点A2017的横坐标为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上A，B两点对应的数分别为a，b，且a，b满足|a+20|=﹣（b﹣13）2，点C对应的数为16，点D对应的数为﹣13．
（1）求a，b的值；
（2）点A，B沿数轴同时出发相向匀速运动，点A的速度为6个单位/秒，点B的速度为2个单位/秒，若t秒时点A到原点的距离和点B到原点的距离相等，求t的值；
（3）在（2）的条件下，点A，B从起始位置同时出发．当A点运动到点C时，迅速以原来的速度返回，到达出发点后，又折返向点C运动．B点运动至D点后停止运动，当B停止运动时点A也停止运动．求在此过程中，A，B两点同时到达的点在数轴上对应的数．
相关试题
