搜索
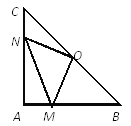
【题目】在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。
（1）写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由；
（2）如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。
参考答案：
【答案】(1)OA=OB=OC. (2)△OMN为等腰直角三角形.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半，直接得出OA=OB=OC；
(2)连接OA，证△ANO≌△BMO，即可得出ON=OM，∠MON=90°，从而△OMN是等腰直角三角形.
（1）
.
（2）
.
证明：
.
,
,
,
,
,
,
≌
.
, 
,
.
.
故答案为：（1）OA=OC=OB (2)OMN为等腰直角三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE=
AC，连接AE交OD于点F，连接CE、OE．（1）求证：OE=CD；
（2）若菱形ABCD的边长为2，∠ABC=60°，求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
ABCD中，E为对角线AC延长线上的一点．(1)若四边形ABCD是菱形，求证：BE＝DE.
(2)写出(1)的逆命题，并判断其是真命题还是假命题，若是真命题，给出证明；若是假命题，举出反例．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1=∠2．
（1）若CE=1，求BC的长；
（2）求证：AM=DF+ME．
-
科目： 来源： 题型：
查看答案和解析>>【题目】济南大明湖畔的“超然楼”被称作“江北第一楼”，某校数学社团的同学对超然楼的高度进行了测量，如图，他们在A处仰望塔顶，测得仰角为30°，再往楼的方向前进60m至B处，测得仰角为60°，若学生的身高忽略不计，
≈1.7，结果精确到1m，则该楼的高度CD为（ ） 
A.47m
B.51m
C.53m
D.54m -
科目： 来源： 题型：
查看答案和解析>>【题目】在边长为2的正方形ABCD中，点P、Q分别是边AB、BC上的两个动点（与点A、B、C不重合），且始终保持BP=BQ，AQ⊥QE，QE交正方形外角平分线CE于点E，AE交CD于点F，连结PQ.
（1）求证：△APQ≌△QCE；
（2）求∠QAE的度数；
（3）设BQ=x，当x为何值时，QF∥CE，并求出此时△AQF的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形
中，
，
，点
从点
出发，以
的速度沿
向点
运动，设点的运动时间为
秒：（1）
________
;(用的代数式表示)（2）当
为何值时，
≌
；（3）当点
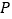从点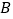开始运动，同时，点
从点出发，以
的速度沿
向点
运动，是否存在这样的
值，使得与
全等？若存在，请求出的值；若不存在，请说明理由.
相关试题
