【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒:
秒:
(1)![]() ________
________![]() ;(用的代数式表示)
;(用的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() ≌
≌![]() ;
;
(3)当点![]() 从点
从点![]() 开始运动,同时,点
开始运动,同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,是否存在这样的
运动,是否存在这样的![]() 值,使得
值,使得![]() 与
与![]() 全等?若存在,请求出
全等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

参考答案:
【答案】(1)(10-2t);(2)当t=2.5时,△ABP≌△DCP.理由见解析;(3)v等于2或2.4时△ABP与△PCQ全等.
【解析】
试题(1)根据P点的运动速度可得BP的长,再利用BC-BP即可得到CP的长;
(2)当t=2.5时,△ABP≌△DCP,根据三角形全等的条件可得当BP=CP时,再加上AB=DC,∠B=∠C可证明△ABP≌△DCP;
(3)此题主要分两种情况①当BP=CQ,AB=PC时,△ABP≌△PCQ;当BA=CQ,PB=PC时,△ABP≌△QCP,然后分别计算出t的值,进而得到v的值.
试题解析:(1)依题可得:BP=2t,
又∵BC= 10cm,
∴CP=10-2t,
故答案为:(10-2t);
(2)当t=2.5时,△ABP≌△DCP.理由如下:
∵t=2.5,
∴BP=2t=2×2.5=5,
∴PC=10-5-5,
在△ABP和△DCP中,
∵ ,
,
∴△ABP≌△DCP(SAS);
(3)①当BP=CQ,AB=CP时,△ABP≌△PCQ,
∵AB=6,BC= 10cm,
∴PC=6,
∴BP=10-6=4,
依题可得:2t=4,
∴t=2,
∴CQ=BP=4,
∴2v=4,
∴v=2;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC, BC= 10cm ,
∴PB=PC=![]() BC=5,
BC=5,
依题可得:2t=5,
∴t=2.5,
∴CQ=BA=6,
∴2.5v=6,
∴v=2.4,
综上所述:当v等于2或2.4时△ABP与△PCQ全等.
-
科目: 来源: 题型:
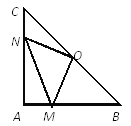
查看答案和解析>>【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,
 ≈1.7,结果精确到1m,则该楼的高度CD为( )
≈1.7,结果精确到1m,则该楼的高度CD为( ) 
A.47m
B.51m
C.53m
D.54m -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合),且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.
(1)求证:△APQ≌△QCE;
(2)求∠QAE的度数;
(3)设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )

A.
B.4
C.2
D.
-
科目: 来源: 题型:
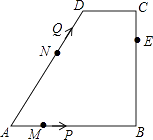
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A.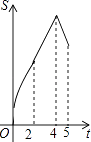
B.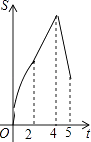
C.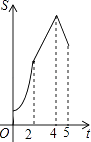
D.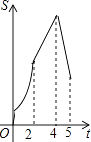
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

