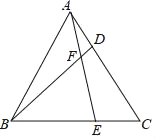
【题目】如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.
(1)∠BFE的度数是多少;
(2)如果![]() ,那么
,那么![]() 等于多少;
等于多少;
(3)如果![]() 时,请用含n的式子表示AF,BF的数量关系,并证明.
时,请用含n的式子表示AF,BF的数量关系,并证明.
参考答案:
【答案】(1)∠BFE=60°;(2)![]() =1;(3)
=1;(3)![]() .证明见解析.
.证明见解析.
【解析】
(1)易证△ABD≌△ACE,可得∠DAF=∠ABF,根据外角等于不相邻两个内角的和即可解题.
(2)如图1中,当![]() =
=![]() 时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;
时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;
(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,由△ABD≌△CAE,推出BD=AE,设BD=AE=m,利用相似三角形的性质,列出关系式即可解决问题;
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAD=∠C=60°,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS)
∴∠DAF=∠ABD,
∴∠BFE=∠ABD+∠BAF=∠DAF+∠BAF=∠BAD=60°,
(2)如图1中,当![]() =
=![]() 时,由题意可知:AD=CD,BE=CE.
时,由题意可知:AD=CD,BE=CE.
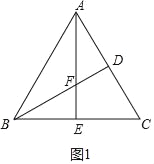
∵△ABC是等边三角形,BE=EC,AD=CD,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() ×60°=30°,∠ABD=
×60°=30°,∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∴∠FAB=∠FBA,
∴FA=FB,
∴![]() =1.
=1.
(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,
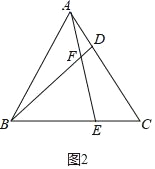
∵△ABD≌△CAE,
∴BD=AE,∠DAF=∠ABD,设BD=AE=m,
∵∠ADF=∠BDA,
∴△ADF∽△BDA,
∴![]() ,
,
∴![]() ①,
①,
∵∠FBE=∠CBD,∠BFE=∠C=60°,
∴△BFE∽△BCD,
∴![]() ,
,
∴![]() ②,
②,
①÷②得到:![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
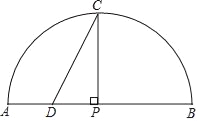
查看答案和解析>>【题目】如图,P是弧AB所对弦AB上一动点,过点P作PC⊥AB交弧AB于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)
小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小凡的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm
0
1
2
3
4
5
6
y/cm
0
2.2
3.2
3.4
3.3
3
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为多少cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+3a过点A(﹣1,0).
(1)求抛物线的对称轴;
(2)直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C.如果该抛物线与线段BC有交点,结合函数的图象,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D(
 ,
, ),E(0,2
),E(0,2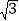 ),F(﹣2,0).
),F(﹣2,0).(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的“等径点”是哪几个点;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是函数y=
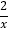 的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则S= .
的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则S= .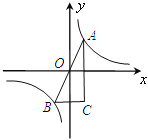
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
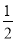 x与双曲线y=
x与双曲线y=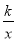 (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.(1)求k的值;
(2)若双曲线y=
 (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.
相关试题

