Question

【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，请根据图象解决下列问题：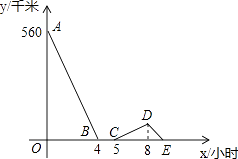

（1）甲乙两地之间的距离为千米；
（2）求快车和慢车的速度；
（3）求线段DE所表示的y与x之间的函数关系式，并写出自变量x的取值范围.

Answer 1

【答案】
（1）560
（2）解：由题意可得出：慢车往返分别用了4小时，慢车行驶4小时的距离，快车3小时即可行驶完，

∴设慢车速度为3xkm/h，快车速度为4xkm/h，

∵由题意可得出：快车行驶全程用了7小时，

∴快车速度为： =80（km/h），

∴4x=80

∴x=20

∴慢车速度为：3x=3×20=60（km/h）

（3）解：由题意可得出：当行驶7小时后，慢车距离甲地60km，

∴D（8，60）

∵慢车往返各需4小时，

∴E（9，0）， 设DE的解析式为：y=kx+b，

∴ ， 解得： ．

∴线段DE所表示的y与x之间的函数关系式为：y=﹣60x+540（8≤x≤9）

【解析】（1）根据图像得到甲乙两地之间的距离；（2）由题意可得到慢车往返分别用了4小时，慢车行驶4小时的距离，快车3小时即可行驶完；求出快车和慢车的速度；（3）根据题意得到当行驶7小时后，慢车距离甲地60km，得到D的坐标，由慢车往返各需4小时，得到E点坐标，求出线段DE所表示的y与x之间的函数关系式.