【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣![]() x+
x+![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).

(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x+1;(2)点P坐标为(3,
x+1;(2)点P坐标为(3,![]() );(3)点Q坐标为(9,4)或(15,16).
);(3)点Q坐标为(9,4)或(15,16).
【解析】试题分析:(1)抛物线顶点在x轴上则可得出顶点纵坐标为0,将解析式进行配方就可以求出a的值,继而得出函数解析式;(2)作出B点关于l的对称点B′,连接EB′交l于点P,如图所示,,三角形BEP为顶点的三角形的周长最小,再求出直线B′E的解析式,进而得出P点坐标;(3)先求出直线FD的解析式,结合以线段FQ为直径的圆恰好经过点D这个条件,明确∠FDG=90°,得出直线DG解析式的k值与直线FD解析式的k值乘积为﹣1,利用D点坐标求出直线DG解析式,将点Q坐标用抛物线解析式表示后代入DG直线解析式可求出点Q坐标.
试题解析:(1)∵抛物线y=ax2﹣6ax+c(a>0)的顶点A在x轴上
∴配方得y=a(x﹣3)2﹣9a+1,则有﹣9a+1=0,解得a=![]()
∴A点坐标为(3,0),抛物线m的解析式为y=![]() x2﹣
x2﹣![]() x+1;
x+1;
(2)∵点B关于对称轴直线x=3的对称点B′为(6,1)
∴连接EB′交l于点P,如图所示

设直线EB′的解析式为y=kx+b,把(﹣7,7)(6,1)代入得
![]() 解得
解得 ,
,
则函数解析式为y=﹣![]() x+
x+![]()
把x=3代入解得y=![]() ,
,
∴点P坐标为(3,![]() );
);
(3)∵y=﹣![]() x+
x+![]() 与x轴交于点D,
与x轴交于点D,
∴点D坐标为(7,0),
∵y=﹣![]() x+
x+![]() 与抛物线m的对称轴l交于点F,
与抛物线m的对称轴l交于点F,
∴点F坐标为(3,2),
求得FD的直线解析式为y=﹣![]() x+
x+![]() ,若以FQ为直径的圆经过点D,可得∠FDQ=90°,则DQ的直线解析式的k值为2,
,若以FQ为直径的圆经过点D,可得∠FDQ=90°,则DQ的直线解析式的k值为2,
设DQ的直线解析式为y=2x+b,把(7,0)代入解得b=﹣14,则DQ的直线解析式为y=2x﹣14,
设点Q的坐标为(a,![]() ),把点Q代入y=2x﹣14得
),把点Q代入y=2x﹣14得
![]() =2a﹣14
=2a﹣14
解得a1=9,a2=15.
∴点Q坐标为(9,4)或(15,16).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在△OBC中,点A是BO延长线上的一点,
(1)
 , Q是BC边上一点,连结AQ交OC边于点P,如图(2),若
, Q是BC边上一点,连结AQ交OC边于点P,如图(2),若 = .猜测:
= .猜测:  的大小关系是 ;
的大小关系是 ;(2)将图(2)中的CO延长到点D,AQ延长到点E,连结DE,得到图(3),则
 等于图中哪三个角的和?并说明理由;
等于图中哪三个角的和?并说明理由;(3)求图(3)中
 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=
 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 =
= ,则b的值是 .
,则b的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长为整数a,b,c,且满足a2+b2-6a-4b+13=0,则c为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】若 2 是方程 x2-2x+c=0 的根,则 c 的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
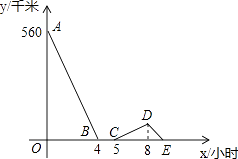
(1)甲乙两地之间的距离为千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
相关试题

