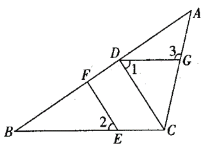
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1)求证: CD∥EF
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数
(3)若BC=6cm,△ABC的面积是12cm2 ,则点A到直线BC的距离是多少?
参考答案:
【答案】(1)见解析;(2)115°;(3)4cm.
【解析】
(1)根据CD⊥AB,EF⊥AB可得∠CDB =∠EFB=90°,然后根据平行线的判定定理可得CD∥EF;
(2)先根据平行线的判定和性质证明DG∥BC,即可得到∠ACB=∠3=115°;
(3)根据三角形面积计算方法即可求出点A到直线BC的距离.
证明:(1) ∵CD⊥AB,EF⊥AB (已知)
∴∠CDB =∠EFB=90°
∴CD∥EF
(2) ∵CD∥EF
∴∠DCB=∠2
∵∠1=∠2
∴∠1=∠DCB
∴DG∥BC
∴∠ACB=∠3=115°
(3)设所求距离为h,则由![]()
解得 h=4
∴点A到直线BC的距离是4cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解全年级学生英语作业的完成情况,帮助英语学习成绩差的学生尽快提高成绩,班主任和英语教师从全年级
 名学生中抽取
名学生中抽取 名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占
名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占 ,明显高于他平时观察到的比例,请回答下列问题:
,明显高于他平时观察到的比例,请回答下列问题:(1)英语教师所用的调查方式是_______;
(2)如果老师的英语作业检查只得“差”的同学有
 名,那么估计全年级的英语作业中可能有多少同学得“差”;
名,那么估计全年级的英语作业中可能有多少同学得“差”;(3)通过问卷调查,老师得到的数据与事实不符,请你解释这个统计数字失真的原因.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在"元旦"期间,几名学生随同家长一起到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几名成人,几名学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.

解:∵EF∥AD(已知)
∴∠2=_________( )
∵∠1=∠2(已知)
∴∠1=__________( )
∴DG∥BA ( )
又∵∠BAC=70°(已知)
∴∠AGD=_________°( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B=
 ∠D,∠C=
∠D,∠C= ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.

求证:四边形DBCF是半对角四边形;
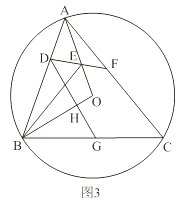
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
相关试题

