【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

参考答案:
【答案】(1)证明见解析;(2)①AQ﹣AP=PQ,②AQ﹣BQ=PQ,③DP﹣AP=PQ,④DP﹣BQ=PQ.
【解析】试题分析:(1)利用AAS证明△AQB≌△DPA,可得AP=BQ;(2)根据AQ﹣AP=PQ和全等三角形的对应边相等可写出4对线段.
试题解析:(1)在正方形中ABCD中,AD=BA,∠BAD=90°,∴∠BAQ+∠DAP=90°,∵DP⊥AQ,∴∠ADP+∠DAP=90°,∴∠BAQ=∠ADP,∵AQ⊥BE于点Q,DP⊥AQ于点P,∴∠AQB=∠DPA=90°,∴△AQB≌△DPA(AAS),
∴AP=BQ.(2)①AQ﹣AP=PQ,②AQ﹣BQ=PQ,③DP﹣AP=PQ,④DP﹣BQ=PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E , BE交CD于点F , ∠1+∠2=90°.
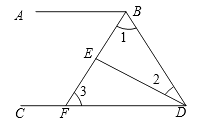
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】若把36°36′36″化成以度为单位,则结果为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.

(1)说明:DC∥AB;
(2)求∠PFH的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
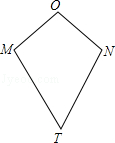
(1)探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=10,BC=CD,BC>AB,BD、AC为对角线,BD=16.
①若∠ABC=90°,求AC的长;
②过点B作BF⊥CD于F,BF交AC于点E,连接DE.当四边形ABED为菱形时,求点F到AB的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的余角的3倍比它的补角的2倍少120°,则这个角的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为( )

A.1:2:3
B.2:1:3
C.3:2:1
D.3:1:2
相关试题

