【题目】如图,∠ABD和∠BDC的平分线交于E , BE交CD于点F , ∠1+∠2=90°.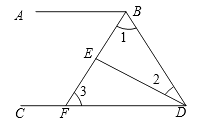
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
参考答案:
【答案】
(1)
证明:(1)∵BE、DE平分∠ABD、∠BDC,
∴∠1=![]() ∠ABD,∠2=
∠ABD,∠2=![]() ∠BDC;
∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
(2)
∵∠1+∠2=90°,∠2=25°,
∴∠ABF=∠1=65°,
∵AB∥CD,
∴∠ABF+∠BFC=180°,
则∠BFC=115°.
【解析】(1)从角平分线的性质可得∠1=![]() ∠ABD,∠2=
∠ABD,∠2=![]() ∠BDC;根据∠1+∠2=90°,得∠ABD+∠BDC=180°,从而得AB∥CD;
∠BDC;根据∠1+∠2=90°,得∠ABD+∠BDC=180°,从而得AB∥CD;
(2)根据平行线的性质去做.
【考点精析】本题主要考查了平行线的判定与性质和角平分线的性质定理的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.
-
科目: 来源: 题型:
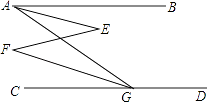
查看答案和解析>>【题目】已知,如图,∠BAG=45°,∠AGD=135°,∠E=∠F.求证:∠BAE=∠CGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行线被第三条直线所截,若同旁内角的度数比是7∶11,则这两个角的度数分别为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
﹣(3a2﹣4ab)+[a2﹣2(2a+2ab)],其中a=﹣2,b=3. -
科目: 来源: 题型:
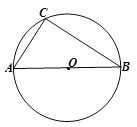
查看答案和解析>>【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
-
科目: 来源: 题型:
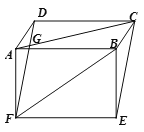
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数:3,0,﹣10,0.58,﹣(﹣6),﹣|﹣9|,(﹣4)2 中,负数有( )
A.1个
B.2个
C.3个
D.4个
相关试题

