【题目】如图,由一个边长为a的小正方形与两个长、宽分别为a,b的小长方形拼接成大长方形ABCD,则整个图形可表达出一些有关多项式因式分解的等式,请你写出其中任意三个等式:__________________________.

参考答案:
【答案】答案不唯一,如a2+2ab=a(a+2b);a(a+b)+ab=a(a+2b);a(a+2b)-a(a+b)=ab
【解析】
根据计算面积的方法多种多样,因此可以用不同的方式表达求解.
把图形分割成一个正方形,两个长方形计算面积,则有:a2+2ab=a(a+2b);
把图形分割成两个长方形,一边长分别是a+b,b,宽都是a,则有:a(a+b)+ab=a(a+2b);
用整个图形的面积减去一个边长为a,a+b的长方形,得到另外一个长方形,边长是a,b,即:a(a+2b)-a(a+b)=ab.
故本题答案为:a2+2ab=a(a+2b);a(a+b)+ab=a(a+2b);a(a+2b)-a(a+b)=ab.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,求d+AB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,扇形AOD中,∠AOD=90°,OA=6,点P为
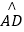 上任意一点(不与点A和D重合),
上任意一点(不与点A和D重合),
PQ⊥OD于点Q,点I为△OPQ的内心,过O、I和D三点的圆的半径为r,则当点P在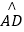 上运动时,求r的值.
上运动时,求r的值.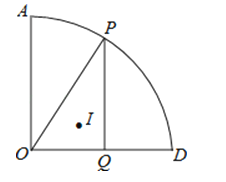
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,
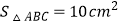 , C△ABC=10cm且∠C=60°.求:
, C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)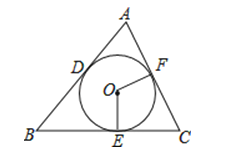
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
(1)求证:AF=BG;
(2)过E点作EH⊥AB于H,试探索线段EH与线段AB的数量关系,并说明理由.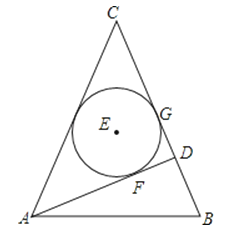
相关试题

