【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

参考答案:
【答案】(1)见解析;(2)结论:DE=2BF.理由见解析.
【解析】
(1)根据题意画出图形即可;
(2)结论:DE=2BF.连接AD,设DE交AC于H.想办法证明△ADH≌△DBF即可解决问题;
解:(1)依题意补全图形如图所示:
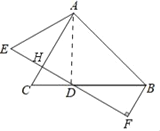
(2)结论:DE=2BF.
理由:连接AD,设DE交AC于H.
∵点E、D关于AC对称,
∴AC垂直平分DE.
∴AE=AD.
∵AE=BD,∴AD=DB.
∴∠DAB=∠ABC=45°.
∴∠ADC=90°.
∴∠ADE+∠BDF=90°.
∵BF⊥ED,AC⊥ED,
∴∠F=∠AHD=90°.
∴∠DBF+∠BDF=90°.
∴∠DBF=∠ADH.
∴△ADH≌△DBF
∴DH=BF
又∵DH=EH,
∴DE=2BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,图中点A表示-36,点B表示44,动点P、Q分别从A、B两点同时出发,相向而行,动点P、Q的运动速度比之是3∶2(速度单位:1个单位长度/秒).12秒后,动点P到达原点O,动点Q到达点C,设运动的时间为t(t>0)秒.
(1)求OC的长;
(2)经过t秒钟,P、Q两点之间相距5个单位长度,求t的值;
(3)若动点P到达B点后,以原速度立即返回,当P点运动至原点时,动点Q是否到达A点,若到达,求提前到达了多少时间,若未能到达,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
(1)求⊙O的半径的长及线段AD的长;
(2)设PH=x,PC=y,求y关于x的函数关系式.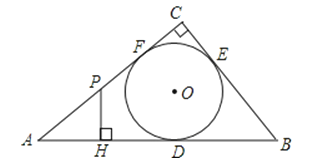
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,求d+AB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由一个边长为a的小正方形与两个长、宽分别为a,b的小长方形拼接成大长方形ABCD,则整个图形可表达出一些有关多项式因式分解的等式,请你写出其中任意三个等式:__________________________.

相关试题

