【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为 ![]() ,依次类推,排在第
,依次类推,排在第 ![]() 位的数称为第
位的数称为第 ![]() 项,记为
项,记为 ![]() .
.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 ![]() 表示(
表示( ![]() ).如:数列1,3,9,27,…为等比数列,其中
).如:数列1,3,9,27,…为等比数列,其中 ![]() ,公比为
,公比为 ![]() .
.
则:
(1)等比数列3,6,12,…的公比 ![]() 为 , 第4项是 .
为 , 第4项是 .
(2)如果一个数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…是等比数列,且公比为
,…是等比数列,且公比为 ![]() ,那么根据定义可得到:
,那么根据定义可得到:![]() ,
, ![]() ,
, ![]() ,……
,…… ![]() .
.
∴ ![]() ,
, ![]() ,
, ![]() ,
, ![]()
由此可得:an=(用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
参考答案:
【答案】
(1)2;24
(2)an=a1qn-1
(3)解:根据题意知,第1项为10÷2=5,第4项为5×23=40
【解析】(1)根据题意知公比q=6÷3=2,第4项是12×2=24;(2)根据定义我们可依次写出这个数列的每一项:a1 , a1q,a1q2 , a1q3 , ….由此可得第n项an=a1qn-1;(1)由第二项除以第一项求出公比q的值,然后用第三项乘以公比2就确定出第4项;
(2)根据定义我们可依次写出这个数列的每一项:a1 , a1q,a1q2 , a1q3 , …从而归纳总结得到通项公式,的右边是一个乘积形式,其中一个因式是a1,另一个因式底数是q,指数比序号小1,从而写出通用公式;
(3)根基定义,由公比q与第二项的值求出第一项的值,进而确定出第4项的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请用两种不同的方法列代数式表示图中阴影部分的面积.

方法①_________________;
方法②_________________;
(2)根据(1)写出一个等式________________;
(3)若
 ,
, .
.①求
 的值。
的值。②
 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:
作物种类
每公顷所需人数/人
每公顷投入资金/万元
蔬菜
4
2
水果
5
3
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,
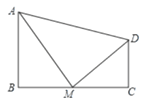
求证:(1) AM⊥DM;
(2) M为BC的中点.
相关试题

