【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
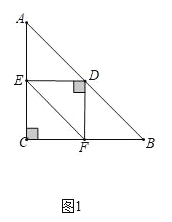
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
参考答案:
【答案】(1)①证明见解析;②![]() ;
;
(2)上述结论成立;理由见解析;
(3)不成立;S△DEF﹣S△CEF=![]() ;理由见解析.
;理由见解析.
【解析】
(1)①先判断出DE∥AC得出∠ADE=∠B,再用同角的余角相等判断出∠A=∠BDF,即可得出结论;②当∠EDF绕D点旋转到DE⊥AC时,四边形CEDF是正方形,边长是AC的一半,即可得出结论;
(2)成立;先判断出∠DCE=∠B,进而得出△CDE≌△BDF,即可得出结论;
(3)不成立;同(2)得:△DEC≌△DBF,得出S△DEF=![]() =S△CFE+
=S△CFE+![]() S△ABC.
S△ABC.
解:(1)①∵∠C=90°,
∴BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴∠ADE=∠B,
∵∠EDF=90°,
∴∠ADE+∠BDF=90°,
∵DE⊥AC,
∴∠AED=90°,
∴∠A+∠ADE=90°,
∴∠A=∠BDF,
∵点D是AB的中点,
∴AD=BD,
在△ADE和△BDF中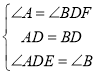 ,
,
∴△ADE≌△BDF(SAS);
②如图1中,当∠EDF绕D点旋转到DE⊥AC时,四边形CEDF是正方形.
设△ABC的边长AC=BC=a,则正方形CEDF的边长为![]() a.
a.
∴S△ABC=![]() a2,S正方形DECF=(
a2,S正方形DECF=(![]() a)2=
a)2=![]() a2,
a2,
即S△DEF+S△CEF=![]() S△ABC;
S△ABC;
故答案为:![]() .
.
(2)上述结论成立;理由如下:连接CD;如图2所示:
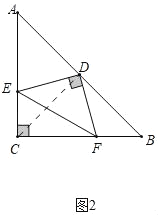
∵AC=BC,∠ACB=90°,D为AB中点,
∴∠B=45°,∠DCE=![]() ∠ACB=45°,CD⊥AB,CD=
∠ACB=45°,CD⊥AB,CD=![]() AB=BD,
AB=BD,
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中,
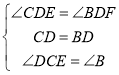 ,
,
∴△CDE≌△BDF(ASA),
∴S△DEF+S△CEF=S△ADE+S△BDF=![]() S△ABC;
S△ABC;
(3)不成立;S△DEF﹣S△CEF=![]() S△ABC;理由如下:连接CD,如图3所示:
S△ABC;理由如下:连接CD,如图3所示:

同(2)得:△DEC≌△DBF,∠DCE=∠DBF=135°
∴S△DEF=S五边形DBFEC,
=S△CFE+S△DBC,
=S△CFE+![]() S△ABC,
S△ABC,
∴S△DEF﹣S△CFE=![]() S△ABC.
S△ABC.
∴S△DEF、S△CEF、S△ABC的关系是:S△DEF﹣S△CEF=![]() S△ABC.
S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图

(1)分别写出下列各点的坐标:A′______;B′______;C′______
(2)若点P(m,n)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为______.
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.

(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请用两种不同的方法列代数式表示图中阴影部分的面积.

方法①_________________;
方法②_________________;
(2)根据(1)写出一个等式________________;
(3)若
 ,
, .
.①求
 的值。
的值。②
 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为 ,依次类推,排在第
,依次类推,排在第  位的数称为第
位的数称为第  项,记为
项,记为  .
.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 表示(
表示(  ).如:数列1,3,9,27,…为等比数列,其中
).如:数列1,3,9,27,…为等比数列,其中  ,公比为
,公比为  .
.
则:
(1)等比数列3,6,12,…的公比 为 , 第4项是 .
为 , 第4项是 .
(2)如果一个数列 ,
,  ,
,  ,
,  ,…是等比数列,且公比为
,…是等比数列,且公比为  ,那么根据定义可得到:
,那么根据定义可得到: ,
, 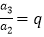 ,
,  ,……
,……  .
.
∴ ,
,  ,
,  ,
, 
由此可得:an=(用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
相关试题

