【题目】某物流公司要同时运输A、B两种型号的商品共13件,A型商品每件体积为2m3 , 每件质量为1吨;B型商品每件体积为0.8m3 , 每件质量为0.5吨,这两种型号商品体积之和不超过18.8m3 , 质量之和大于8.5吨.
(1)求A、B两种型号商品的件数共有几种可能?写出所有可能情况;
(2)若一件A型商品运费为200元,一件B型商品运费为180元.则(1)中哪种情况的运费最少?最少运费是多少?
参考答案:
【答案】
(1)
解:设A型商品x件,B型商品(13﹣x)件.
由题意可得: ![]() ,
,
解得:4<x≤7,
∴A、B两种型号商品的件数共有3种可能
所有可能情况为:A,5件,B,8件;A,6件,B,7件;A,7件,B,6件
(2)
解:∵一件A型商品运费为200元,一件B型商品运费为180元,
∴A商品越少则总运费越少,
∴当A,5件,B,8件时运费最低,最少运费是:200×5+8×180=2440(元)
【解析】(1)根据不等关系式为:2×A型商品件数+0.8×B型商品件数≤18.8,1×A型商品件数+0.5×B型商品件数>8.5,进而求出即可;(2)根据A型,B型商品运费得出A商品越少则总运费越少,进而求出即可.
-
科目: 来源: 题型:
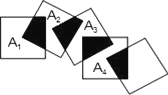
查看答案和解析>>【题目】将五个边长都为2的正方形按如图所示摆放,点A1、A2、A3、A4分别是四个正方形的中心,则图中四块阴影部分的面积的和为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC中,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O与点F,点E在AC上,且∠EBC=
 ∠BAC,BE交⊙O于点D.
∠BAC,BE交⊙O于点D.
(1)求证:AB=AE;
(2)若AB=10,cos∠EBC= ,求线段BE和BC的长.
,求线段BE和BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BF,∠1与∠2互补.
(1)试说明:FG∥AB;
(2)若∠CFG=60°,∠2=150°,则DE与AC垂直吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD中,点E、F分别在边DC、AD上,且AE⊥BF于G.

(1)求证:BF=AE;
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立?(直接写结论)
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ:S正方形ABCD . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.

(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
相关试题

