【题目】已知:如图△ABC中,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O与点F,点E在AC上,且∠EBC= ![]() ∠BAC,BE交⊙O于点D.
∠BAC,BE交⊙O于点D.
(1)求证:AB=AE;
(2)若AB=10,cos∠EBC= ![]() ,求线段BE和BC的长.
,求线段BE和BC的长.
参考答案:
【答案】
(1)
证明:连接AD,
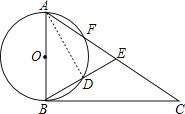
∵AB为直径,
∴∠ADB=90°=∠ADE,
∴∠DAB+∠ABD=90°,
∵BC切⊙O于B,
∴∠ABD+∠EBC=90°,
∴∠EBC=∠BAD,
∵∠EBC= ![]() ∠BAC,
∠BAC,
∴∠EAD=∠BAD,
在△ABD和△AED中

∴△ABD≌△AED(ASA),
∴AB=AE.
(2)
解: 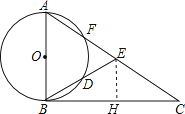 ∵∠EBC=∠BAD,AB=10,cos∠EBC=
∵∠EBC=∠BAD,AB=10,cos∠EBC= ![]() ,
,
∴在Rt△BAD中,cos∠BAD= ![]() =
= ![]() ,
,
∴AD=4 ![]() ,
,
由勾股定理得:BD=2 ![]() ,
,
∵△ABD≌△AED,
∴BD=DE,
∴BE=2BD=4 ![]() ,
,
过E作EH⊥BC于H,
则EH∥AB,
∵cos∠EBC= ![]() ,BE=4
,BE=4 ![]() ,
,
∴BH=BEcos∠EBC=8,
由勾股定理得:EH= ![]() =4,
=4,
∵EH∥AB,
∴△CHE∽△CBA,
∴ ![]()
∴ ![]() ,
,
∴CH=5 ![]() ,
,
∴BC=8+5 ![]() =13
=13 ![]() .
.
【解析】(1)连接AD,求出∠EBC=∠BAD,推出∠BAD=∠EAD,证出△ABD≌△AED即可.(2)根据∠EBC=∠BAD,AB=10,cos∠EBC= ![]() 求出AD,根据勾股定理求出BD,即可求出答案,求出EH,BH,根据相似求出CH,即可求出答案.
求出AD,根据勾股定理求出BD,即可求出答案,求出EH,BH,根据相似求出CH,即可求出答案.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据2013﹣2017年某市财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
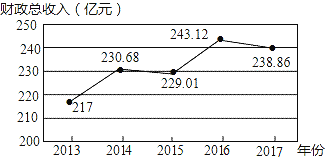
A. 2013~2017年财政总收入呈逐年增长
B. 预计2018年的财政总收入约为253.43亿元
C. 2014~2015年与2016~2017年的财政总收入下降率相同
D. 2013~2014年的财政总收入增长率约为6.3%
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟
0<x≤5
5<x≤10
10<x≤15
15<x≤20
频数(通话次数)
20
16
9
5
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
-
科目: 来源: 题型:
查看答案和解析>>【题目】将五个边长都为2的正方形按如图所示摆放,点A1、A2、A3、A4分别是四个正方形的中心,则图中四块阴影部分的面积的和为______.
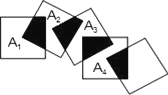
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BF,∠1与∠2互补.
(1)试说明:FG∥AB;
(2)若∠CFG=60°,∠2=150°,则DE与AC垂直吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司要同时运输A、B两种型号的商品共13件,A型商品每件体积为2m3 , 每件质量为1吨;B型商品每件体积为0.8m3 , 每件质量为0.5吨,这两种型号商品体积之和不超过18.8m3 , 质量之和大于8.5吨.
(1)求A、B两种型号商品的件数共有几种可能?写出所有可能情况;
(2)若一件A型商品运费为200元,一件B型商品运费为180元.则(1)中哪种情况的运费最少?最少运费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD中,点E、F分别在边DC、AD上,且AE⊥BF于G.

(1)求证:BF=AE;
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立?(直接写结论)
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ:S正方形ABCD .
相关试题

