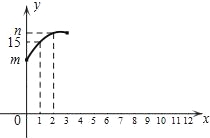
【题目】为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的还车数比借车数的2倍少4,求此时段的借车数.
参考答案:
【答案】(1)13,7:00时自行车的存量;(2) y=﹣![]() x2+
x2+![]() x+13;(3)10:00﹣11:00这个时段的借车数为3辆.
x+13;(3)10:00﹣11:00这个时段的借车数为3辆.
【解析】
试题分析:(1)根据等量关系式:m+借车数﹣还车数=8:00的存量,列式求出m的值,并写出实际意义;(2)先求出9点时自行车的存量,当x=2时所对应的y值,即求出n的值;再设一般式将三点坐标代入求出解析式;(3)先分别计算9:00﹣10:00和10:00﹣11:00的自行车的存量,即当x=3和x=4时所对应的y值,设10:00﹣11:00这个时段的借车数为x,根据上一时段的存量+还车数﹣借车数=此时段的存量,列式求出x的值即可.
试题解析:解:(1)m+7﹣5=15,m=13,
则m的实际意义:7:00时自行车的存量;
故答案为:13,7:00时自行车的存量;
(2)由题意得:n=15+8﹣7=16,
设二次函数的关系式为:y=ax2+bx+c,
把(0,13)、(1,15)和(2,16)分别代入得: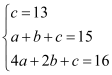 ,
,
解得: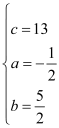 ,
,
∴y=﹣![]() x2+
x2+![]() x+13;
x+13;
(3)当x=3时,y=﹣![]() ×32+
×32+![]() ×3+13=16,
×3+13=16,
当x=4时,y=﹣![]() ×42+
×42+![]() ×4=13=15,
×4=13=15,
设10:00﹣11:00这个时段的借车数为x,则还车数为2x﹣4,
根据题意得:16+2x﹣4﹣x=15,
x=3,
答:10:00﹣11:00这个时段的借车数为3辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连接CD.
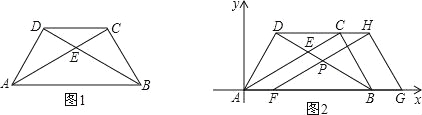
(1)填空:如图1,AC的长度= ,tan∠ABD= ;
(2)试判断△ADC与△AEB的关系,并说明理由;
(3)如图2建立平面直角坐标系,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=t,△FBP面积为S,求S与t之间的函数关系式,并写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2+4a2=6a4
B.(a+1)2=a2+1
C.(a2)3=a5
D.x7÷x5=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s,在跑步过程中,甲、乙两人之间的距离y(m)与乙出发的时间t(s)之间的关系如图所示.求a,b,c的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a4+a2=a6B.4a2-2a2=2a2C.(a4)2=a6D.a4a2=a8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个选项中,不是y关于x的函数的是( )
A.|y|=x﹣1 B.y=
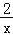 C.y=2x﹣7 D.y=x2
C.y=2x﹣7 D.y=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
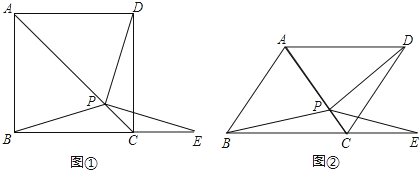
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
相关试题

