【题目】将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连接CD.
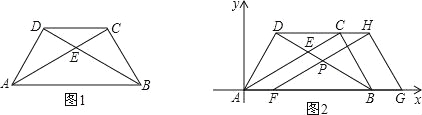
(1)填空:如图1,AC的长度= ,tan∠ABD= ;
(2)试判断△ADC与△AEB的关系,并说明理由;
(3)如图2建立平面直角坐标系,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=t,△FBP面积为S,求S与t之间的函数关系式,并写出t的取值范围.
参考答案:
【答案】(1)4![]() ,
,![]() ;(2)△ADC∽△AEB,理由见解析;(3)S=
;(2)△ADC∽△AEB,理由见解析;(3)S=![]() (8﹣t)2,t的取值范围为:0≤t<8
(8﹣t)2,t的取值范围为:0≤t<8
【解析】
试题分析:(1)首先根据题意得:DC∥AB,∠ADB=∠ACB=90°,∠ABD=∠CAB=30°,然后由勾股定理,求得AC与BD的长,(2)根据两个含30°的直角三角板直接求出∠DAC=∠EAB=30°,∠AEB=∠ADC=120,即可得出△ADC∽△AEB.(3)过P作出△FBP的高.△FBP面积应等于FB×PK÷2,易得FB=AB﹣AF=8﹣t;则KB等于FB的一半,利用30°的正切值可求得FK的值.
试题解析:(1)根据题意得:DC∥AB,∠ADB=∠ACB=90°,∠ABD=∠CAB=30°,
∵AB=8,BC=AD=4,
∴AC=BD=4![]() ,∠ABD=30°,
,∠ABD=30°,
∴tan∠ABD=tan30°=![]() ,
,
(2)△ADC∽△AEB,
理由:∵∠BAD=∠ABC=60°,∠BAC=∠ABD=30°,
∴∠DAC=∠CBD=∠BAC=30°,AE=BE,
∴∠AEB=180°﹣∠EAB﹣∠EBA=120°,
∵AC=BD,
∴ED=EC,
∴∠BDC=∠ACD=![]() (180°﹣∠DEC)=30°,
(180°﹣∠DEC)=30°,
∵∠ADB=90°
∴∠ADC=∠ADB+∠BDC=120°=∠AEB,
∵∠DAC=∠BAC,
∴△ADC∽△AEB,
(3)(3)由题意知,FP∥AE,
∴∠1=∠PFB,
又∵∠1=∠2=30°,
∴∠PFB=∠2=30°,
∴FP=BP
过点P作PK⊥FB于点K,则FK=BK=![]() FB.
FB.
∵AF=t,AB=8,
∴FB=8﹣t,BK=![]() (8﹣t).
(8﹣t).
在Rt△BPK中,PK=BKtan∠2=![]() (8﹣t)tan30°=
(8﹣t)tan30°=![]() (8﹣t).
(8﹣t).
∴△FBP的面积S=![]() FBPK=
FBPK=![]() (8﹣t)
(8﹣t)![]() (8﹣t),
(8﹣t),
∴S与t之间的函数关系式为:
S=![]() (8﹣t)2,
(8﹣t)2,
t的取值范围为:0≤t<8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子(1)2x﹣7≥﹣3,(2)
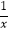 ﹣x>0,(3)7<9,(4)x2+3x>1,(5)
﹣x>0,(3)7<9,(4)x2+3x>1,(5) ﹣2(a+1)≤1,(6)m﹣n>3,中是一元一次不等式的有( )
﹣2(a+1)≤1,(6)m﹣n>3,中是一元一次不等式的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】仔细观察,思考下面一列数有哪些规律,﹣2,4,﹣8,16,﹣32,64,…然后填出下面两空:(1)第7个数是;(2)第n个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:﹣3(2a2﹣2ab)+4(a2+ab﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2+4a2=6a4
B.(a+1)2=a2+1
C.(a2)3=a5
D.x7÷x5=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s,在跑步过程中,甲、乙两人之间的距离y(m)与乙出发的时间t(s)之间的关系如图所示.求a,b,c的值.

-
科目: 来源: 题型:
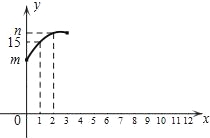
查看答案和解析>>【题目】为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段
x
还车数
借车数
存量y
7:00﹣8:00
1
7
5
15
8:00﹣9:00
2
8
7
n
…
…
…
…
…
根据所给图表信息,解决下列问题:
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的还车数比借车数的2倍少4,求此时段的借车数.
相关试题

