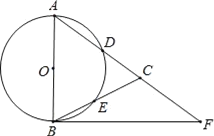
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)利用已知条件证得△AGC∽△ABF,利用比例式求得线段的长即可.
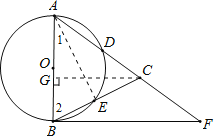
试题解析:(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=![]() ∠CAB.
∠CAB.
∵∠CBF=![]() ∠CAB,
∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)过点C作CG⊥AB于G.
∵sin∠CBF=![]() ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1=![]() ,
,
∵在Rt△AEB中,∠AEB=90°,AB=5,
∴BE=ABsin∠1=![]() ,
,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2![]() ,
,
在Rt△ABE中,由勾股定理得AE=![]() ,
,
∴sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,
,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴![]()
∴BF=![]() .
.
-
科目: 来源: 题型:
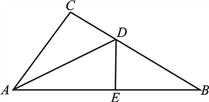
查看答案和解析>>【题目】如图,在直角△ABC中,∠C=90°,DE垂直平分AB,交BC于点D、交AB于点E.
(1)若AD平分∠CAB,则∠B的度数是 度;
(2)若AB=10,△ACD的周长为14,求△ACB的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
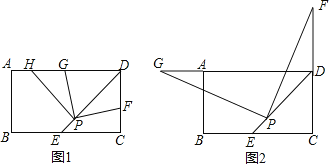
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF;
②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DE、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+3和2a﹣15是一个数的两个平方根,则这个数是( )
A.4
B.7
C.16
D.49 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形对应角平分线的比是4:9,那么它们的周长比是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(1﹣2m)x+m﹣1,若函数y随x的增大而减小,并且函数的图像经过二、三、四象限,求m的取值范围.
相关试题

