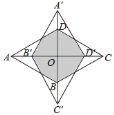
【题目】如图,菱形ABCD的一个内角是60,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为![]() ,则菱形ABCD的边长为_________.
,则菱形ABCD的边长为_________.
参考答案:
【答案】2
【解析】
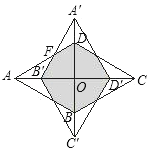
根据已知可得重叠部分是个八边形,根据其周长从而可求得其一边长即可得到答案.
因为旋转前后两菱形重叠部分多边形的周长为![]() ,
,
∴根据旋转的性质可得阴影部分为各边长相等的八边形,
∴B′F=FD=![]() ,
,
∵菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′,
∴∠DAO=∠B′A′O=30°,
∴∠A′B′C=60°,
∴∠AFB′=∠A′B′C-∠DAO=30°,
∴AB′=B′F=FD=![]() ,
,
∵DO=OB′=![]() AD,AO=
AD,AO=![]() AD,
AD,
∴AO=AB′+OB′=![]() +
+![]() AD,
AD,
∴![]() AD=
AD=![]() +
+![]() AD,
AD,
∴AD=2,
故答案为:2.
-
科目: 来源: 题型:
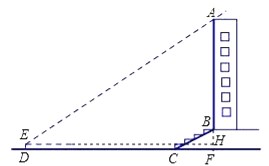
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:
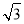 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
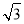 ≈1.73.)
≈1.73.)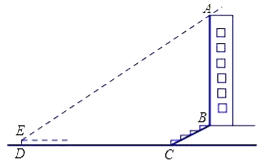
【答案】33.3.
【解析】
试题分析:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
试题解析:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,
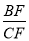 =i=1:
=i=1: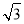 ,∴设BF=k,则CF=
,∴设BF=k,则CF=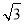 k,BC=2k.
k,BC=2k.又∵BC=12,∴k=6,∴BF=6,CF=
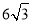 .∵DF=DC+CF,∴DF=40+
.∵DF=DC+CF,∴DF=40+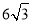 .∵在Rt△AEH中,tan∠AEH=
.∵在Rt△AEH中,tan∠AEH=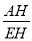 ,∴AH=tan37°×(40+
,∴AH=tan37°×(40+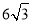 )≈37.8(米),∵BH=BF﹣FH,∴BH=6﹣1.5=4.5.∵AB=AH﹣HB,∴AB=37.8﹣4.5=33.3.
)≈37.8(米),∵BH=BF﹣FH,∴BH=6﹣1.5=4.5.∵AB=AH﹣HB,∴AB=37.8﹣4.5=33.3.答:大楼AB的高度约为33.3米.
考点:1.解直角三角形的应用-仰角俯角问题;2.解直角三角形的应用-坡度坡角问题.
【题型】解答题
【结束】
24【题目】为迎接安顺市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
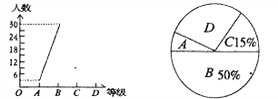
(2)补全折线统计图;
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________;
(4)若等级A为优秀,求该班的优秀率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为______.

-
科目: 来源: 题型:
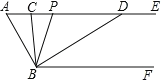
查看答案和解析>>【题目】如图,已知AE∥BF,∠A=60°,点P为射线AE上任意一点(不与点A重合),BC,BD分别平分∠ABP和∠PBF,交射线AE于点C,点D.
(1)图中∠CBD= °;
(2)当∠ACB=∠ABD时,∠ABC= °;
(3)随点P位置的变化,图中∠APB与∠ADB之间的数量关系始终为 ,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若
 ,则下列不等式中不一定成立的是( )
,则下列不等式中不一定成立的是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 度;
(2)求∠CAE的度数.

相关试题

