搜索
【题目】如图，在△ABC中，AD是BC边上的高，将△ABD沿AD折叠得到△AED，点E落在CD上，∠B=50°，∠C=30°．
（1）填空：∠BAD= 度；
（2）求∠CAE的度数．
参考答案：
【答案】（1）40；（2）20°
【解析】
（1）直接根据三角形内角和定理求出∠BAD的度数；
（2）先根据图形折叠的性质求出∠AED的度数，再由三角形外角的性质即可得出结论．
（1）∵AD是BC边上的高，∠B=50°，
∴∠BAD=180°-90°-50°=40°．
故答案为：40；
（2）∵△AED是由△ABD折叠得到，
∴∠AED=∠B=50°，
∵∠AED是△ACE的外角，
∴∠AED=∠CAE+∠C，
∴∠CAE=∠AED-∠C=50°-30°=20°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,菱形ABCD的一个内角是60,将它绕对角线的交点O顺时针旋转90后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为
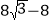，则菱形ABCD的边长为_________.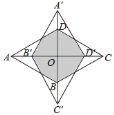
-
科目： 来源： 题型：
查看答案和解析>>【题目】“一带一路”国际合作高峰论坛期间，我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区，已知2件甲种商品与3件乙种商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元.
（1）甲种商品与乙种商品的销售单价各多少元？
（2）若甲、乙两种商品的销售总收入不低于4200万元，则至少销管甲种商品多少万件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若
，则下列不等式中不一定成立的是（ ）A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为迎接安顺市文明城市创建工作，某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动，成绩分为A、B、C、D四个等级，并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息，解答下列各题:
(1)求八年一班共有多少人；
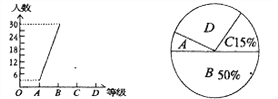
(2)补全折线统计图；
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________；
(4)若等级A为优秀，求该班的优秀率.
【答案】（1）60；（2）补图见解析；（3）108°；（4）5%.
【解析】（1）用B等人数除以其所占的百分比即可得到总人数；
（2）用求得的总人数乘以C等所占的百分比即可得到C等的人数，总人数减去A、C等的人数即可求得D等的人数；
（3）用D等的人数除以总人数乘以360°即可得到答案；
（4）用A等的人数除以总人数乘以100%即可得到答案． 解答：
解：(1)30÷50%=60(人)
∴八年级一共有60人。
(2)等级为“C”的人数为60×15%=9(人).
等级为“D”的人数为603309=18(人).
补全折线统计图如下。
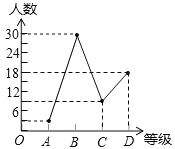
(3)等极为“D”的部分所占圆心角的度数为
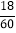×360°=108°，故答案为：108°.
(4)该班的优秀率
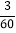×100%=5%.∴该班的优秀率为5%.
点睛：本题考查统计相关知识.利用拆线图与扇形图得出相关信息是解题的关键.
【题型】解答题
【结束】
25【题目】已知抛物线y=ax2+bx+c经过A（﹣1，0），B（3，0），C（0，3）三点，直线L是抛物线的对称轴．
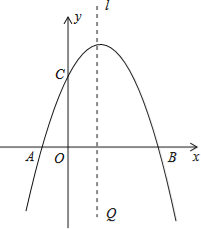
（1）求抛物线的函数关系式；
（2）求抛物线的顶点坐标；
（3）设P点是直线L上的一个动点，当△PAC的周长最小时，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以圆O为圆心，半径为1的弧交坐标轴于A，B两点，P是弧
上一点（不与A，B重合），连接OP，设∠POB=α，则点P的坐标是 
A. （sinα，sinα） B. （cosα，cosα） C. （cosα，sinα） D. （sinα，cosα）
-
科目： 来源： 题型：
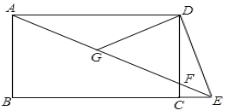
查看答案和解析>>【题目】如图，点E是矩形ABCD的边BC延长线上一点，连接AE，交CD于点F，G是AF的中点，再连接DG、DE，且DE=DG.
(1)求证：∠DEA=2∠AEB；
(2)若BC=2AB，求∠AED的度数。
相关试题
