【题目】如图,![]() ,
,![]() ,AE平分
,AE平分![]() ,
,![]() ,交AC延长线于F,且垂足为E,则下列结论:
,交AC延长线于F,且垂足为E,则下列结论:![]() ;
;![]() ;
;![]() ,
,![]() ;
;![]() 其中正确的结论有______
其中正确的结论有______![]() 填写序号
填写序号![]()

参考答案:
【答案】①③⑤
【解析】
试题根据∠ACB=90°,BF⊥AE,得出∠ACB=∠BED=∠BCF=90°,推出∠F=∠ADC,证△BCF≌△ACD,根据全等三角形的性质即可判断①②;假如AC+CD=AB,求出∠F+∠FBC≠90°,和已知矛盾,即可判断③④,证根据全等三角形的判定ASA得出△BEA≌△FEA,推出BE=EF,即可判断⑤.
解:∵∠ACB=90°,BF⊥AE,
∴∠ACB=∠BED=∠BCF=90°,
∴∠F+∠FBC=90°,∠BDE+∠FBC=90°,
∴∠F=∠BDE,
∵∠BDE=∠ADC,
∴∠F=∠ADC,
∵AC=BC,
∴△BCF≌△ACD,
∴AD=BF,∴①正确;②错误;
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
假如AC+CD=AB,
∴AB=AF,∴∠F=∠FBA=65°,
∴∠FBC=65°﹣45°=20°,
∴∠F+∠FBC≠90°,∴③错误;④错误;
由△BCF≌△ACD,
∴AD=BF,
∵AE平分∠BAF,AE⊥BF,
∴∠BEA=∠FEA=90°,∠BAE=∠FAE,
∵AE=AE,∴△BEA≌△FEA,
∴BE=EF,
∴⑤正确;
故答案为:①③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上张老师将课本44页第4题进行了改编,图形不变.请你完成下问题.


(1)如图1,∠ACB=∠ADB,BC=BD,求证:△ABC≌△ABD.
(2)如图2,∠CAB=∠DAB,BC=BD,求证:△ABC≌△ABD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ).
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ).①作出AD的依据是SAS;②∠ADC=60°
③点D在AB的中垂线上;④S△DAC:S△ABD=1:2.

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
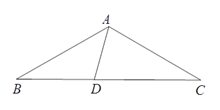
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣2与y轴的交点为A,抛物线的顶点为B(1,﹣3).
(1)求出抛物线的解析式;
(2)点P为x轴上一点,当三角形PAB的周长最小时,求出点P的坐标;
(3)水平移动抛物线,新抛物线的顶点为C,两抛物线的交点为D,当O,C,D在一条直线上时,请直接写出平移的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
相关试题

