【题目】如图,抛物线y=ax2+bx﹣2与y轴的交点为A,抛物线的顶点为B(1,﹣3).
(1)求出抛物线的解析式;
(2)点P为x轴上一点,当三角形PAB的周长最小时,求出点P的坐标;
(3)水平移动抛物线,新抛物线的顶点为C,两抛物线的交点为D,当O,C,D在一条直线上时,请直接写出平移的距离.

参考答案:
【答案】(1) y=(x﹣1)2﹣3=x2﹣2x﹣2 (2) P(![]() ,0) (3) 平移距离为2或3
,0) (3) 平移距离为2或3
【解析】
(1)根据题意可得点A的坐标为(0,﹣2),根据顶点坐标为(1,﹣3),可得设抛物线解析式y=a(x﹣1)2﹣3把A点的坐标代入求得a值,即可得抛物线的解析式;(2)当PA+PB最小时,△ABP的周长最小,作A点关于x轴的对称点A'(0,2),连接A'B,用待定系数法求得直线A'B的解析式,直线A'B与x轴的交点坐标即为点P的坐标;(3)设抛物线向右平移m个单位,得到新的抛物线的顶点C(1+m,-3),由此可得新抛物线的解析式,把两个抛物线的解析式联立组成方程组,解方程组求得点D的坐标,再求得直线OC的解析式,因O、C、D三点共线,可得以m为未知数的方程,解方程求得m的值即可.
(1)根据题意得:A(0,﹣2),
设抛物线解析式y=a(x﹣1)2﹣3过点A(0,﹣2),
∴﹣2=a﹣3,
∴a=1,
∴抛物线解析式y=(x﹣1)2﹣3=x2﹣2x﹣2;
(2)∵A(0,﹣2),B(1,﹣3),
∴AB=![]() ,
,
∵△ABP的周长=PA+PB+AB=PA+PB+![]() ,
,
∴当PA+PB最小时,△ABP的周长最小;
作A点关于x轴的对称点A'(0,2),连接A'B,
设直线A'B解析式y=kx+b,
根据题意得:![]() ,
,
解得:k=﹣5,b=2
∴直线A'B的解析式y=﹣5x+2;
当y=0时,x=![]() ,
,
∴P(![]() ,0);
,0);
(3)设向右平移m个单位长度,则所得新的抛物线的顶点C(1+m,-3),
∴平移后抛物线解析式y=(x﹣1﹣m)2﹣3,
∴C(1+m,﹣3),
∴根据题意可得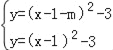 ,
,
∴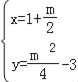 ,
,
∴D(1+![]() ,
,![]() );
);
∵C(1+m,﹣3,),O(0,0),
∴直线CO解析式y=![]() x,
x,
∵O,C,D三点共线,
∴![]() =
=![]() ,
,
解得:m1=0(不合题意舍去),m2=﹣3,m3=2;
∴向右平移2个单位长度,或向左平移3个单位长度,O,C,D三点共线.
∴平移距离为2或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
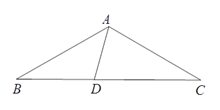
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,AE平分
,AE平分 ,
, ,交AC延长线于F,且垂足为E,则下列结论:
,交AC延长线于F,且垂足为E,则下列结论: ;
; ;
; ,
, ;
; 其中正确的结论有______
其中正确的结论有______ 填写序号
填写序号

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC与△DBC中,∠ACB=∠DBC=90°,E是BC的中点,EF⊥AB,AB=DE.
(1)求证:BC=DB;
(2)若BD=8cm,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
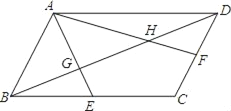
A.
 B.
B.  C.
C.  D.
D. 
相关试题

