【题目】创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为 ![]() ;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为
;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为 ![]() .
.
(1)请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?
(2)若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算)
参考答案:
【答案】
(1)解:九(一)班制作的“文明劝导员”胸章和“文明监督岗” 胸章分别为x只、y只,
根据题意得:  解得:
解得: ![]() 经检验符合题意,
经检验符合题意,
所以九(一)班制作了“文明劝导员” 胸章5只、“文明监督岗” 胸章10只
(2)解:由题可知,盒中剩余的“文明劝导员” 胸章和“文明监督岗” 胸章分别为2只、3只,我们不妨把两只“文明劝导员” 胸章记为a1、a2;3只“文明监督岗” 胸章记为b1、b2、b3,则可列出表格如下:
a1 | a2 | b1 | b2 | b3 | |
a1 | a1 a2 | a1b1 | a1b2 | a1b3 | |
a2 | a2 a1 | a2 b1 | a2 b2 | a2 b3 | |
b1 | b1 a1 | b1a2 | b1 b2 | b1 b3 | |
b2 | b2 a1 | b2a2 | b2b1 | b2 b3 | |
b3 | b3 a1 | b3a2 | b3b1 | b3b2 |
∴ ![]()
【解析】(1)九(一)班制作的“文明劝导员”胸章和“文明监督岗” 胸章分别为x只、y只,根据概率公式由前后两次概率的值列出二元一次方程组,求解检验即可;
(2)由题可知,盒中剩余的“文明劝导员” 胸章和“文明监督岗” 胸章分别为2只、3只,我们不妨把两只“文明劝导员” 胸章记为a1、a2;3只“文明监督岗” 胸章记为b1、b2、b3,则可列出表格,由表格可知所有均可能结果共20种,其中文明劝导员”胸章、“文明监督岗”胸章各1只的情况共12种,根据概率公式计算即可。
【考点精析】认真审题,首先需要了解列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率),还要掌握概率公式(一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.

(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【概念学习】
规定:求若干个相同的有理数(均不等
 )的除法运算叫做除方,如2÷2÷2,
)的除法运算叫做除方,如2÷2÷2,  等.类比有理数的乘方,我们把
等.类比有理数的乘方,我们把 记作
记作 ,读作“
,读作“ 的圈
的圈 次方”,
次方”,  记作
记作 ,读作“
,读作“ 的圈
的圈 次方”.一般地,把
次方”.一般地,把 (
( )记作
)记作 读作“
读作“ 的圈
的圈 次方”
次方”【初步探究】
(1)直接写出计算结果:
 =_____,
=_____, 
 _____
_____(2)关于除方,下列说法错误的是(______)
A.任何非零数的圈2次方都等于1
B.对于任何正整数
 ,
, 
C.

D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘法运算呢?


(3)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式
 =_________
=_________(4)想一想:将一个非零有理数
 的圈n次方写成幂的形式等于_________
的圈n次方写成幂的形式等于_________(5)算一算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8)、动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动、其中,点M沿OA向终点A运动,点N沿BC向终点C运动、过点N作NP⊥BC,交AC于P,连结MP、已知动点运动了t秒、

(1)P点的坐标为( , )(用含t的代数式表示);
(2)试求 △MPA面积的最大值,并求此时t的值;
(3)请你探索:当t为何值时,△MPA是一个等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:抛物线y=-
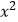 +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC=
+bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= 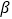 ,tanα-tanβ=2,∠ACB=90°.
,tanα-tanβ=2,∠ACB=90°.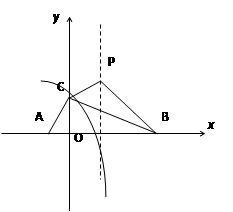
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,∠ABC=90°.以AB为斜边作等腰直角三角形ADB.点P是直线DB上一个动点,连接AP,作PE⊥AP交BC所在的直线于点E.

(1)如图1,点P在BD的延长线上,PE⊥EC,AD=1,直接写出PE的长;
(2)点P在线段BD上(不与B,D重合),依题意,将图2补全,求证:PA=PE;
(3)点P在DB的延长线上,依题意,将图3补全,并判断PA=PE是否仍然成立.
相关试题

