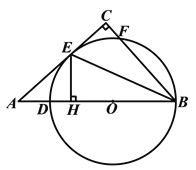
【题目】如图,在△![]() 中,∠
中,∠![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 相切于点
相切于点![]() ,与边
,与边![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)连接OE.由切线的性质得到OE⊥AC,从而有OE∥BC,由平行线的性质得到∠OEB=∠CBE.再由等腰三角形的性质得到∠OEB=∠OBE,即有∠OBE=∠CBE,由角平分线的性质即可得出结论;
(2)解Rt△ABC得到AB的长.再由OE∥BC,得到△AEO∽△ACB,由相似三角形对应边成比例,得到OB的长,进而可得出结论.
详解:(1)连接OE.
∵⊙O与边AC相切,∴OE⊥AC.
∵∠C=90°,∴OE∥BC,∴∠OEB=∠CBE.
∵OB=OE,∴∠OEB=∠OBE,∴∠OBE=∠CBE.
∵EH⊥AB,∴EH=EC.
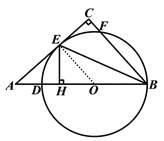
(2)在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ∥
∥![]() ,∴△AEO∽△ACB,
,∴△AEO∽△ACB,
∴![]() ,即
,即![]() .
.
解得:![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,点P是射线BA上的一个动点,以BP为半径的
,点P是射线BA上的一个动点,以BP为半径的 交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点
交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点 ,连结
,连结 ,
, ,设直线
,设直线 与直线BC交于点F.
与直线BC交于点F. 当点P在线段BA上时,
当点P在线段BA上时, 求证:
求证: ;
; 连结
连结 ,当
,当 时,求
时,求 的长;
的长; 连结AD,AF,当
连结AD,AF,当 恰为等边三角形时,求此时四边形
恰为等边三角形时,求此时四边形 的面积;
的面积; 当四边形
当四边形 在
在 内部时,请直接写出BP的取值范围.
内部时,请直接写出BP的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为

A. 1或
 B. -
B. -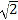 或
或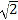 C.
C. 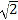 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地走去,y1,y2分别表示小东、小明离B地的距离y(km)与所用时间x(h)的关系,如图所示,根据图象提供的信息,回答下列问题:

(1)试用文字说明交点P所表示的实际意义;
(2)求y1与x的函数关系式;
(3)求A,B两地之间的距离及小明到达A地所需的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线
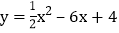 的顶点M在直线L:
的顶点M在直线L: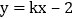 上.
上. 求直线L的函数表达式;
求直线L的函数表达式;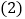 现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当
现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当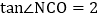 时,求平移后的抛物线的解析式.
时,求平移后的抛物线的解析式.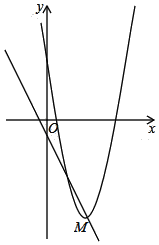
-
科目: 来源: 题型:
查看答案和解析>>【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:
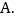 非常了解,
非常了解, 比较了解,
比较了解,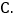 基本了解,
基本了解,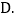 不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.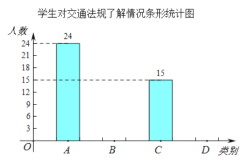

请结合图中所给信息解答下列问题:
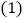 本次共调查______名学生;扇形统计图中C所对应扇形的圆心角度数是______;
本次共调查______名学生;扇形统计图中C所对应扇形的圆心角度数是______; 补全条形统计图;
补全条形统计图; 该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有多少名?
该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有多少名?
相关试题

