【题目】已知抛物线y=(m-1)x2+m2-2m-2的图象开口向下,且经过点(0,1).
(1)求m的值;
(2)求此抛物线的顶点坐标及对称轴;
(3)当x为何值时,y随x的增大而增大?
参考答案:
【答案】(1) m=-1;(2) (3) 见解析
【解析】试题分析:开口向下说明m-1<0,将(0,1)代入函数表达式可求出m的值;函数表达式为y=-2x2+1,可求得对称轴是y轴,顶点坐标是(0,1);开口向下,对称轴是y轴,所以在y轴左侧,y随x的增大而增大。
解:(1)由题意,得![]() ,
,
解得m=-1.
(2)当m=-1时,抛物线的表达式为y=-2x2+1,其顶点坐标为(0,1),对称轴为y轴.
(3)因为抛物线y=-2x2+1的开口向下,所以在对称轴的左侧,即当x<0时,y随x的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年2月初,在抵御新冠肺炎的工作中,全国各地口罩严重供应不足,某乡镇企业缝纫车间立即转岗做口罩以供应本地志愿者和卫生系统,该车间有技术工人15人,生产部为了合理制定口罩的日生产定额,统计了15人某天加工口罩数如下:
车间15名工人某一天加工口罩个数统计表
加工零件数/个
540
450
300
240
210
120
人数
1
1
2
6
3
2
(1)求这一天15名工人加工口罩数的平均数、中位数和众数.
(2)为了提高大多数工人的积极性,管理者准备试行“每天定额生产,超产有奖”的措施,假如你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

-
科目: 来源: 题型:
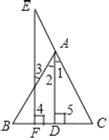
查看答案和解析>>【题目】已知,如图所示,AD⊥BC于D,EF⊥BC于F,∠3=∠E,说明AD是∠BAC的角平分线请你完成下列说理过程(在横线上填上适当的内容,在括号内写出说理依据).
理由:∵AD⊥BC,EF⊥BC(已知)
∴∠4=∠5=90°( ),
∴AD∥EF( ),
∴∠1= ( ),
∠2= ( ),
又∵∠E=∠3(已知)
∴ ( ),
即AD是∠BAC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 点
点 的坐标分别为
的坐标分别为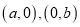 ,且
,且 将线段
将线段 绕点
绕点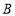 逆时针旋转
逆时针旋转 得到线段
得到线段 .
.(1)直接写出
 __,
__, __ _,点
__ _,点 的坐标为 _;
的坐标为 _;(2)如图2,作
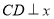 轴于点
轴于点 点
点 是
是 的中点,点
的中点,点 在
在 内部,
内部, 求证:
求证:
(3)如图3,点
 是第二象限内的一个动点,若
是第二象限内的一个动点,若 求线段
求线段 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
 中,点
中,点 在边
在边 上,
上, 交
交 于点
于点 .
.(1)如图1,连接
 ,求证:
,求证: ;
;
(2)如图2,点
 在
在 上,
上, 交
交 于点N,
于点N,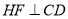 交
交 于点
于点 ,求证:
,求证: ;
;
(3)如图3,点
 在
在 的延长线上,
的延长线上, 在直线
在直线 的右侧作
的右侧作 且
且
 为线段
为线段 的中点,当点
的中点,当点 从点
从点 运动到点
运动到点 时,写出点
时,写出点 运动的路径长并简要说明理由.
运动的路径长并简要说明理由.
相关试题

