【题目】在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,连接![]() ,求证:
,求证:![]() ;
;

(2)如图2,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点N,
于点N,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 在直线
在直线![]() 的右侧作
的右侧作![]() 且
且![]()
![]() 为线段
为线段![]() 的中点,当点
的中点,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,写出点
时,写出点![]() 运动的路径长并简要说明理由.
运动的路径长并简要说明理由.

参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() ;理由见解析.
;理由见解析.
【解析】
(1)如图1中,只要证明![]() 即可解决问题.
即可解决问题.
(2)如图2中,连接![]() ,作
,作![]() 于
于![]() .利用平行线等分线段定理解决问题即可.
.利用平行线等分线段定理解决问题即可.
(3)如图3中,连接![]() ,
,![]() ,作
,作![]() 交
交![]() 于
于![]() .利用全等三角形的性质证明
.利用全等三角形的性质证明![]() ,点
,点![]() 的运动轨迹是线段
的运动轨迹是线段![]() ,求出
,求出![]() 的长,利用三角形的中位线定理即可解决问题.
的长,利用三角形的中位线定理即可解决问题.
(1)证明:如图1中,

![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)证明:如图2中,连接![]() ,作
,作![]() 于
于![]() .
.

![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(3)解:如图3中,连接![]() ,
,![]() ,作
,作![]() 交
交![]() 于
于![]() .
.

![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 的运动轨迹是线段
的运动轨迹是线段![]() ,
,
![]() 点
点![]() 从
从![]() 运动到
运动到![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() 当点
当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 运动的路径长为
运动的路径长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(m-1)x2+m2-2m-2的图象开口向下,且经过点(0,1).
(1)求m的值;
(2)求此抛物线的顶点坐标及对称轴;
(3)当x为何值时,y随x的增大而增大?
-
科目: 来源: 题型:
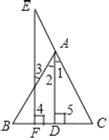
查看答案和解析>>【题目】已知,如图所示,AD⊥BC于D,EF⊥BC于F,∠3=∠E,说明AD是∠BAC的角平分线请你完成下列说理过程(在横线上填上适当的内容,在括号内写出说理依据).
理由:∵AD⊥BC,EF⊥BC(已知)
∴∠4=∠5=90°( ),
∴AD∥EF( ),
∴∠1= ( ),
∠2= ( ),
又∵∠E=∠3(已知)
∴ ( ),
即AD是∠BAC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 点
点 的坐标分别为
的坐标分别为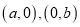 ,且
,且 将线段
将线段 绕点
绕点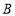 逆时针旋转
逆时针旋转 得到线段
得到线段 .
.(1)直接写出
 __,
__, __ _,点
__ _,点 的坐标为 _;
的坐标为 _;(2)如图2,作
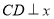 轴于点
轴于点 点
点 是
是 的中点,点
的中点,点 在
在 内部,
内部, 求证:
求证:
(3)如图3,点
 是第二象限内的一个动点,若
是第二象限内的一个动点,若 求线段
求线段 的最大值.
的最大值.
-
科目: 来源: 题型:
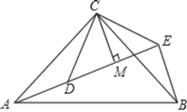
查看答案和解析>>【题目】如图,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)求∠AEB的度数;
(2)线段CM、AE、BE之间存在怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点
中,点 的坐标是
的坐标是 ,则
,则 点的坐标是( )
点的坐标是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把y=
 x2的图象向上平移2个单位.
x2的图象向上平移2个单位.(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x的值.
相关试题

