【题目】如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E. 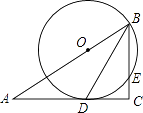
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求AD的长.
参考答案:
【答案】
(1)证明:连接OD,如图,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
∴AC是⊙O的切线
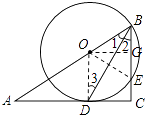
(2)解:过O作OG⊥BC,连接OE,
则四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BC,∠C=90°,
∴OG∥AC,
∴△BOG∽△BAC,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AD= ![]() .
.

【解析】(1)连接OD,由BD为角平分线得到一对角相等,再根据等腰三角形的性质得出一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直角,即可得证;(2)过O作OG垂直于BE,可得出四边形ODCG为矩形,利用勾股定理求出BG的长,根据相似三角形的性质即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
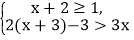 并将解集在数轴上表示出来.
并将解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂在A、B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x 节,试定出用车厢节数x表示总费用y的公式.
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式:
(1)4x>3x+5 (2)-2x<17
(3)0.3x<-0.9 (4)x<
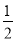 x-4
x-4 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的分式方程
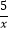 =
=  有解,则字母a的取值范围是( )
有解,则字母a的取值范围是( )
A.a=5或a=0
B.a≠0
C.a≠5
D.a≠5且a≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是定线段OA上的动点,点P从O点出发,沿线段OA运动至点A后,再立即按原路返回至点O停止,点P在运动过程中速度大小不变,以点O为圆心,线段OP长为半径作圆,则该圆的周长l与点P的运动时间t之间的函数图象大致为( )
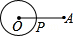
A.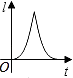
B.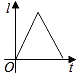
C.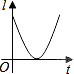
D.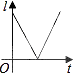
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)( x-y)7÷(y-x)2÷( x-y)3;
(2)
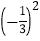 +
+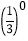 +
+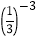 ;
;(3)( -2)0-
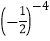 +
+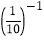 +
+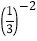 ·
·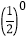 ;
;(4) a4m+1÷(-a) 2m+1 (m为正整数).
相关试题

