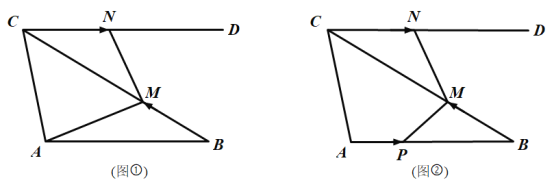
【题目】如图①,在![]() 中,
中,![]() cm ,
cm ,![]() cm,过点
cm,过点![]() 作射线
作射线![]() .点
.点![]() 从点
从点![]() 出发,以3 cm/s的速度沿
出发,以3 cm/s的速度沿![]() 匀速移动;点
匀速移动;点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿
cm/s的速度沿![]() 匀速移动.点
匀速移动.点![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止移动.连接
同时停止移动.连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() (s).
(s).
(1)点![]() 、
、![]() 从移动开始到停止,所用时间为 s;
从移动开始到停止,所用时间为 s;
(2)当![]() 与
与![]() 全等时,
全等时,
①若点![]() 、
、![]() 的移动速度相同,求
的移动速度相同,求![]() 的值;
的值;
②若点![]() 、
、![]() 的移动速度不同,求
的移动速度不同,求![]() 的值;
的值;
(3)如图②,当点![]() 、
、![]() 开始移动时,点
开始移动时,点![]() 同时从点
同时从点![]() 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿![]() 向点
向点![]() 匀速移动,到达点
匀速移动,到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 返回.当点
返回.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 、
、![]() 同时停止移动.在移动的过程中,是否存在
同时停止移动.在移动的过程中,是否存在![]() 与
与![]() 全等的情形?若存在,求出
全等的情形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)①t=
;(2)①t=![]() ;②a=
;②a=![]() ;(3)t=6.4或t=
;(3)t=6.4或t=![]()
【解析】
(1)根据时间=路程÷速度即可求得答案;
(2)①由题意得:BM=CN=3t,则只可以是△CMN≌△BAM,AB=CM,由此列出方程求解即可;
②由题意得:CN≠BM,则只可以是△CMN≌△BMA,AB=CN=12,CM=BM,进而可得3t=10,求解即可;
(3)分情况讨论,当△CMN≌△BPM时,BP=CM,若此时P由A向B运动,则12-2t=20-3t,但t=8不符合实际,舍去,若此时P由B向A运动,则2t-12=20-3t,求得t=6.4;当△CMN≌△BMP时,则BP=CN,CM=BM,可得3t=10,t=![]() ,再将t=
,再将t=![]() 代入分别求得AP,BP的长及a的值验证即可.
代入分别求得AP,BP的长及a的值验证即可.
解:(1)20÷3=![]() ,
,
故答案为:![]() ;
;
(2)∵CD∥AB,
∴∠B=∠DCB,
∵△CNM与△ABM全等,
∴△CMN≌△BAM或△CMN≌△BMA,
①由题意得:BM=CN=3t,
∴△CMN≌△BAM
∴AB=CM,
∴12=20-3t,
解得:t=![]() ;
;
②由题意得:CN≠BM,
∴△CMN≌△BMA,
∴AB=CN=12,CM=BM,
∴CM=BM=![]() BC,
BC,
∴3t=10,
解得:t=![]()
∵CN=at,
∴![]() a=12
a=12
解得:a=![]() ;
;
(3)存在
∵CD∥AB,
∴∠B=∠DCB,
∵△CNM与△PBM全等,
∴△CMN≌△BPM或△CMN≌△BMP,
当△CMN≌△BPM时,则BP=CM,
若此时P由A向B运动,则BP=12-2t,CM=20-3t,
∵BP=CM,
∴12-2t=20-3t,
解得:t=8 (舍去)
若此时P由B向A运动,则BP=2t-12,CM=20-3t,
∵BP=CM,
∴2t-12=20-3t,
解得:t=6.4,
当△CMN≌△BMP时,则BP=CN,CM=BM,
∴CM=BM=![]() BC
BC
∴3t=10,
解得:t=![]()
当t=![]() 时,点P的路程为AP=2t=
时,点P的路程为AP=2t=![]() ,
,
此时BP=AB-AP=12-![]() =
=![]() ,
,
则CN=BP=![]()
即at=![]() ,
,
∵t=![]() ,
,
∴a=1.6符合题意
综上所述,满足条件的t的值有:t=6.4或t=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“湘一四边形”.
(1)已知:如图1,四边形
 是“湘一四边形”,
是“湘一四边形”,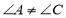 ,
,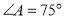 ,
,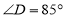 .则
.则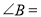 ,
, 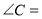 ,若
,若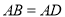 ,
,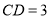 ,则
,则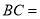 (直接写答案)
(直接写答案)(2)已知:在“湘一四边形”
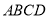 中,
中,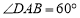 ,
,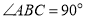 ,
,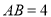 ,
,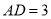 .求对角线
.求对角线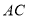 的长(请画图求解),
的长(请画图求解),(3)如图(2)所示,在四边形
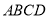 中,若
中,若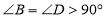 ,当
,当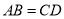 时,此时四边形
时,此时四边形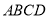 是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.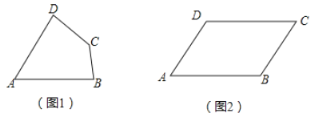
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠CBF=
 ∠CAB.
∠CAB.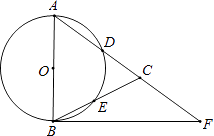
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=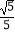 ,求BC和BF的长.
,求BC和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
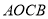 的边
的边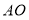 ,
, 在坐标轴上,点
在坐标轴上,点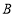 的坐标为
的坐标为 .点
.点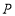 从点
从点 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿 轴向点
轴向点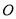 运动;点
运动;点 从点
从点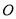 同时出发,以相同的速度沿
同时出发,以相同的速度沿 轴的正方向运动,规定点
轴的正方向运动,规定点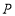 到达点
到达点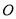 时,点
时,点 也停止运动,连接
也停止运动,连接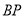 ,过
,过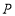 点作
点作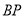 的垂线,与过点
的垂线,与过点 平行于
平行于 轴的直线
轴的直线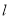 相交于点
相交于点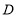 ,
, 与
与 轴交于点
轴交于点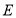 ,连接
,连接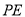 ,设点
,设点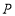 运动的时间为
运动的时间为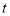 秒.
秒.(1)线段
 (用含
(用含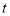 的式子表示),点
的式子表示),点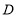 的坐标为 (用含
的坐标为 (用含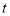 的式子表示),
的式子表示), 的度数为 .
的度数为 .(2)经探究
 周长是一个定值,不会随时间
周长是一个定值,不会随时间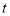 的变化而变化,请猜测周长的值并证明.
的变化而变化,请猜测周长的值并证明.(3)①当
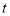 为何值时,有
为何值时,有 .
.②
 的面积能否等于
的面积能否等于 周长的一半,若能求出此时
周长的一半,若能求出此时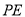 的长度;若不能,请说明理由.
的长度;若不能,请说明理由.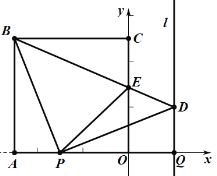
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=6cm,动点P以2cm/s的速度从A﹣B﹣A在线段AB上运动,到达点A后,停止运动;动点Q以1cm/s的速度从B﹣A在线段AB上运动,到达点A后,停止运动.若动点P,Q同时出发,设点Q的运动时间是t(单位:s)时,两个动点之间的距离为S(单位:cm),则能表示S与t的函数关系的是( )

A.
 B.
B.
C.
 D.
D.
相关试题

