【题目】如图,线段AB=6cm,动点P以2cm/s的速度从A﹣B﹣A在线段AB上运动,到达点A后,停止运动;动点Q以1cm/s的速度从B﹣A在线段AB上运动,到达点A后,停止运动.若动点P,Q同时出发,设点Q的运动时间是t(单位:s)时,两个动点之间的距离为S(单位:cm),则能表示S与t的函数关系的是( )
![]()
A. B.
B.
C. D.
D.
参考答案:
【答案】D
【解析】
分别分三个阶段计算和分析两动点之间距离与时间的关系:①P、Q从出发到第一次相遇;②从P、Q第一次相遇到P点到达B地;③从动点P到达点B到动点P返回点A,据此求解.
设点Q的运动时间是t(单位:s)时,两个动点之间的距离为S(单位:cm),
P、Q从出发到第一次相遇:
6=2t+t
解得,t=2
由此可知,刚开始P和Q两点间的距离越来越小直到相遇时,它们之间的距离变为0,此时用的时间为2s;
此时,点P离点B的距离为:6﹣2×2=2cm,点Q离点A的距离为:6﹣2=4cm,
相遇后,点P到达B点用的时间为:2÷2=1s,此时两个动点之间的距离为3cm,
由此可知,相遇后,在第3s时点P到达B点,从相遇到点P到达B点它们的距离在变大,1s后P点从B点返回,点P继续运动,两个动点之间的距离逐渐变小,同时达到A点.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在
 中,
中,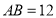 cm ,
cm ,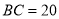 cm,过点
cm,过点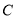 作射线
作射线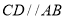 .点
.点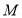 从点
从点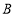 出发,以3 cm/s的速度沿
出发,以3 cm/s的速度沿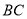 匀速移动;点
匀速移动;点 从点
从点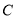 出发,以
出发,以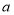 cm/s的速度沿
cm/s的速度沿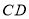 匀速移动.点
匀速移动.点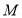 、
、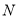 同时出发,当点
同时出发,当点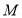 到达点
到达点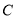 时,点
时,点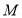 、
、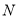 同时停止移动.连接
同时停止移动.连接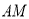 、
、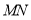 ,设移动时间为
,设移动时间为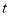 (s).
(s).(1)点
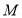 、
、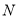 从移动开始到停止,所用时间为 s;
从移动开始到停止,所用时间为 s;(2)当
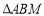 与
与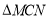 全等时,
全等时,①若点
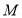 、
、 的移动速度相同,求
的移动速度相同,求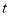 的值;
的值;②若点
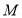 、
、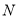 的移动速度不同,求
的移动速度不同,求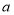 的值;
的值;(3)如图②,当点
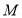 、
、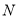 开始移动时,点
开始移动时,点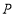 同时从点
同时从点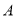 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿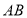 向点
向点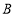 匀速移动,到达点
匀速移动,到达点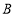 后立刻以原速度沿
后立刻以原速度沿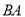 返回.当点
返回.当点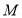 到达点
到达点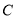 时,点
时,点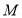 、
、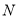 、
、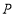 同时停止移动.在移动的过程中,是否存在
同时停止移动.在移动的过程中,是否存在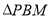 与
与 全等的情形?若存在,求出
全等的情形?若存在,求出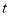 的值;若不存在,说明理由.
的值;若不存在,说明理由.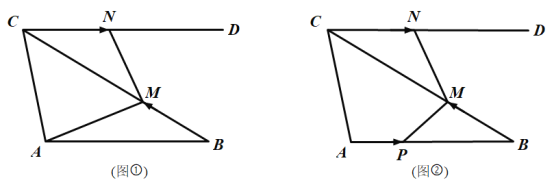
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
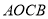 的边
的边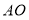 ,
, 在坐标轴上,点
在坐标轴上,点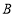 的坐标为
的坐标为 .点
.点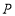 从点
从点 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿 轴向点
轴向点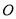 运动;点
运动;点 从点
从点 同时出发,以相同的速度沿
同时出发,以相同的速度沿 轴的正方向运动,规定点
轴的正方向运动,规定点 到达点
到达点 时,点
时,点 也停止运动,连接
也停止运动,连接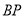 ,过
,过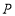 点作
点作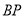 的垂线,与过点
的垂线,与过点 平行于
平行于 轴的直线
轴的直线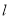 相交于点
相交于点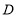 ,
, 与
与 轴交于点
轴交于点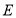 ,连接
,连接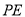 ,设点
,设点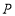 运动的时间为
运动的时间为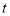 秒.
秒.(1)线段
 (用含
(用含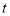 的式子表示),点
的式子表示),点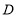 的坐标为 (用含
的坐标为 (用含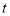 的式子表示),
的式子表示), 的度数为 .
的度数为 .(2)经探究
 周长是一个定值,不会随时间
周长是一个定值,不会随时间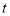 的变化而变化,请猜测周长的值并证明.
的变化而变化,请猜测周长的值并证明.(3)①当
 为何值时,有
为何值时,有 .
.②
 的面积能否等于
的面积能否等于 周长的一半,若能求出此时
周长的一半,若能求出此时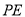 的长度;若不能,请说明理由.
的长度;若不能,请说明理由.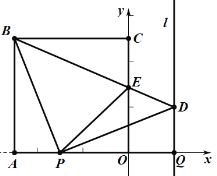
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
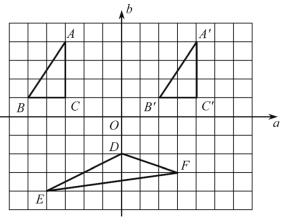
查看答案和解析>>【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的变换得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请求出三角形DEF的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到矩形AnBnCnDn(n>2).

(1)求AB1和AB2的长.
(2)若ABn的长为56,求n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:

(2)当P点从点O出发10秒,可得到的整数点的个数是 个.
(3)当P点从点O出发 秒时,可得到整数点(10 ,5).
相关试题

