【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作ABDE,连接AD、EC. 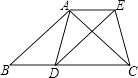
(1)试说明:△ADC≌△ECD;
(2)若BD=CD,试说明:四边形ADCE是矩形.
参考答案:
【答案】
(1)证明:∵AB=AC,
∴∠B=∠ACB,
又∵ABDE中,AB=DE,AB∥DE,
∴∠B=∠EDC=∠ACB,AC=DE,
在△ADC和△ECD中,
 ,
,
∴△ADC≌△ECD(SAS).
(2)解:∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
【解析】(1)利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB,则易证△ADC≌△ECD,利用全等三角形的对应边相等即可证得;(2)根据平行四边形性质推出AE=BD=CD,AE∥CD,得出平行四边形,根据AC=DE推出即可.
【考点精析】利用平行四边形的性质和矩形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的第一条边的长是
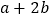 ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。(1)用含
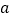 、
、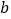 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;(2)当
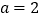 ,
,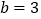 时,求这个三角形的周长;
时,求这个三角形的周长;(3)当
 ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D、E在AB、AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
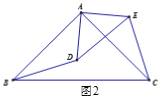
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
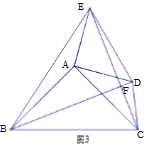
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点. 若BD=
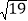 ,求四边形BCDE的面积.
,求四边形BCDE的面积.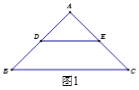
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一快递小哥骑电动车需要在规定的时间把快递送到某地,若他以
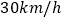 的速度行驶就会提前2分钟到达,如果他以
的速度行驶就会提前2分钟到达,如果他以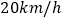 的速度行驶就要迟到6分钟。
的速度行驶就要迟到6分钟。(1)快递小哥行驶的路程是多少千米;
(2)当快递小哥以
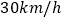 的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。 -
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm.
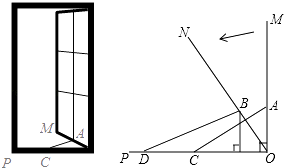
(1)求B点到OP的距离.
(2)求滑动支架AC的长. (参考数据:sin37°=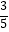 ,cos37°=
,cos37°= 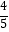 ,tan37°=
,tan37°=  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?
相关试题

