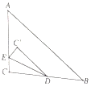
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是BC边的中点,E是AC边上的任意一点,△DCE和△DC′E关于直线DE对称,若点C′ 恰好落在△ABC的中位线上,则CE的长度为_______.
参考答案:
【答案】![]() 或
或![]() .
.
【解析】
分别画了三角形的三条中位线,根据题意C′只能落在DF和FG上,分别画出图形,设CE=x,利用勾股定理列方程求出x的值即可.
解:取AC,AB的中点F,G,连结DF,FG,GD.
① 如图,当点C′落在DF上时,
∵D为BC的中点,
∴DC′=DC=![]() BC=4,
BC=4,
在Rt△ABC中,AC=6,BC=8,
∴AB=![]() =10,
=10,
∵D,F分别为中点,
∴DF=![]() AB=5,
AB=5,
∴FC′= DF- DC′=5-4=1,
设CE=CE′=x,则EF=3-x,
在Rt△EFC′中,
![]() ,
,
∴![]() ,
,
解得,x=![]() ,
,
∴CE=![]() .
.
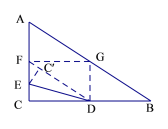
② 如图,当点C′落在FG上时,
∵D,G分别为各边中点,
∴DG=3,
又DC′=DC=4,
在Rt△DGC′中,
![]() =
=![]() ,
,
∵F,G分别为各边中点,
∴FG=![]() BC=4,
BC=4,
∴FC′=FG-GC′=4-![]() ,
,
设EC=EC′=x,则EF=3-x,
在Rt△EFC′中,
![]() ,
,
∴![]() ,
,
解得,x=![]() ,
,
∴CE=![]() .
.

综上,CE的值为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏:
口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀,摸球的人都蒙上眼睛.先甲摸两次,每次摸出一个球;把甲摸出的两个球放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分 ;得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图求甲得1分的概率;
(2)这个游戏是否公平?请说明理由.
-
科目: 来源: 题型:
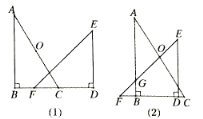
查看答案和解析>>【题目】如图,为一副重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )
A. 3B.
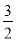 C.
C. 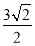 D.
D. 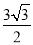
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时)
频数(人数)
频率
2≤t<3
4
0.1
3≤t<4
10
0.25
4≤t<5
a
0.15
5≤t<6
8
b
6≤t<7
12
0.3
合计
40
1
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
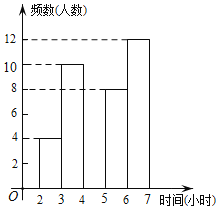
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC=90°, ∠B=30°,高AD与角平分线CE相交于F.
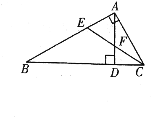
(1)求证△AEF是等边三角形;
(2)EF=2FD.
-
科目: 来源: 题型:
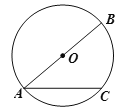
查看答案和解析>>【题目】如图,AC是以AB为直径的⊙O的弦,点D是⊙O上的一点,过点D作⊙O的切线交直线AC于点E,AD平分∠BAE,若AB=10,DE=3,则AE的长为____________.
相关试题

