【题目】如图,四边形ABCD是一个菱形绿地,其周长为40 ![]() m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数) 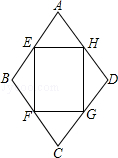
参考答案:
【答案】解:连接BD,AC, ∵菱形ABCD的周长为40 ![]() m,
m,
∴菱形ABCD的边长为10 ![]() m,
m,
∵∠ABC=120°,
∴△ABD,△BCD是等边三角形,
∴对角线BD=10 ![]() m,AC=10
m,AC=10 ![]() m,
m,
∵E,F,G,H是菱形ABCD各边的中点,
∴四边形EFGH是矩形,矩形的边长分别为5 ![]() m,5
m,5 ![]() m,
m,
∴矩形EFGH的面积为5 ![]() ×5
×5 ![]() =50
=50 ![]() (m2),即需投资金为50
(m2),即需投资金为50 ![]() ×10=500
×10=500 ![]() ≈866(元).
≈866(元).
答:需投资金为866元.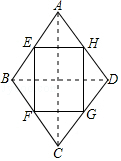
【解析】连接BD,AC,由菱形ABCD的周长求出边长,再由∠ABC的度数确定出三角形ABD与三角形BCD都为等边三角形,进而求出BD与AC的长,由E、F、G、H分别为中点确定出四边形EFGH为矩形,求出矩形边长,进而求出矩形面积,求出所求即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣8y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于C点,AC平分∠DAB.
(1)求证:AD⊥CD;
(2)若AD=2,
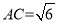 ,求⊙O的半径R的长.
,求⊙O的半径R的长.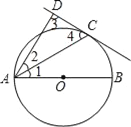
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次12人参加的数学测试中,得100分、95分、90分、85分、75分的人数分别为1、3、4、2、2,那么这组数据的众数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
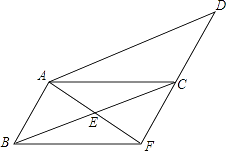
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】截止2013年底,中国高速铁路营运里程达到11000km,居世界首位,将11000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB为锐角,如图(1).
(1)若OM平分∠AOC,ON平分∠BOD,∠MON=32°,∠COD=10°,如图(2)所示,求∠AOB的度数.
(2)若OM,OD,OC,ON是∠AOB的五等分线,如图(3)所示,以射线OA,OM,OD,OC,ON,OB为始边的所有角的和为980°,求∠AOB的度数.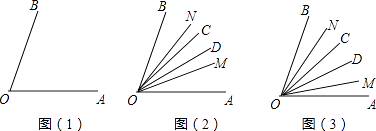
相关试题

