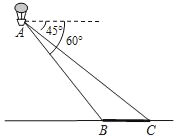
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,![]() ≈1.72).
≈1.72).
参考答案:
【答案】51m
【解析】
作AD⊥CB交CB所在直线于点D,根据等腰直角三角形的性质求出CD,根据正切的定义求出BD,计算即可.
作AD⊥CB交CB所在直线于点D,
由题知,∠ACD=45°,∠ABD=60°,
在Rt△ACD中,∠ACD=45°,
所以CD=AD=120 m,
在Rt△ABD中,∠ABD=60°,tan60°=![]() =
=![]() ,
,
所以BD=![]() =40
=40![]() ,
,
所以BC=CD﹣BD=120﹣40![]() ≈120﹣69.2≈51(m),
≈120﹣69.2≈51(m),
答:大桥BC的长度约为51m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
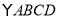 中,
中, 是
是 边上一点,
边上一点,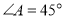 ,
,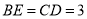 ,
, ,点
,点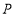 ,
,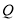 分别是
分别是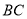 ,
,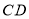 边上的动点,且始终保持
边上的动点,且始终保持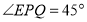 .
.

(1)求
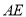 的长;
的长;(2)若四边形
 为平行四边形时,求
为平行四边形时,求 的周长;
的周长;(3)将
 沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段
沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
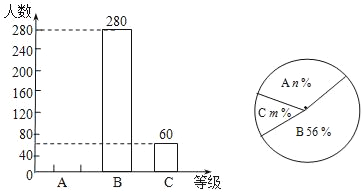
(1)本次调查的人数为 ;
(2)补全条形统计图;
(3)若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个,黑球2个.
(1)若先从袋中取出x(x>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则x的值为 ;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用画树状图或列表法求这个事件的概率.
-
科目: 来源: 题型:
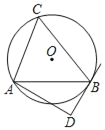
查看答案和解析>>【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.
(1)求k的值;
(2)设抛物线与直线y=﹣
 (x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,
(x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b, )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
)两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;(3)将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.
相关试题

