搜索
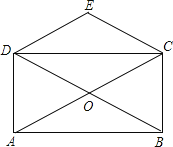
【题目】如图，矩形ABCD的对角线AC、BD交于点O，CE∥BD，DE∥AC．
（1）证明：四边形OCED为菱形；
（2）若AC=4，求四边形CODE的周长．
参考答案：
【答案】(1)见解析； (2)8.
【解析】（1）由CE∥BD，DE∥AC可得四边形OCED是平行四边形，由四边形ABCD是矩形可得OD=OC，从而可得平行四边形OCED是菱形；
（2）由AC=4，四边形ABCD是矩形可得OC=2，结合四边形CODE是菱形可得四边形CODE的周长是：2×4=8.
（1）∵CE∥BD，DE∥AC，
∴四边形CODE为平行四边形，
∵四边形ABCD是矩形，
∴OD=OC，
∴四边形CODE为菱形；
（2）∵四边形ABCD是矩形，
∴OC=OD=
AC，
又∵AC=4，
∴OC=2，
由（1）知，四边形CODE为菱形，
∴四边形CODE的周长为=4OC=2×4=8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝kx＋6分别与x轴、y轴交于点E，F，已知点E的坐标为（－8，0），点A的坐标为（－6，0）．
（1）求k的值；
（2）若点P（x，y）是该直线上的一个动点，探究：当△OPA的面积为27时，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，两个形状、大小完全相同的含有30゜和60゜的三角板如图放置，PA、PB与直线MN重合，且三角板PAC，三角板PBD均可以绕点P逆时针旋转．
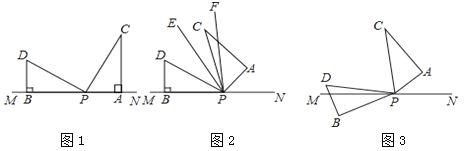
（1）试说明：∠DPC=90゜；
（2）如图2，若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度，PF平分∠APD，PE平分∠CPD，求∠EPF；
（3）如图3，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为3゜/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为2゜/秒，在两个三角板旋转过程中（PC转到与PM重合时，两三角板都停止转动），以下两个结论：①
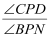为定值；②∠BPN+∠CPD为定值，请选出正确的结论，并说明理由． -
科目： 来源： 题型：
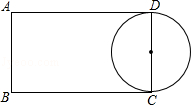
查看答案和解析>>【题目】如图，矩形ABCD中，AB=4，AD=7，点E，F分别在边AD、BC上，且B、F关于过点E的直线对称，如果以CD为直径的圆与EF相切，那么AE= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为
、
、
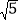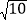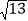，求△ABC的面积．小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法．
请回答：
（1）①图1中△ABC的面积为________；
②图1中过O点画一条线段MN，使MN＝2AB，且M、N在格点上．
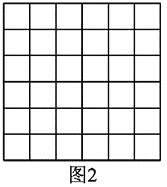
（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．利用构图法在图2中画出三边长分别为
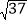、2、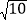
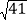的格点△DEF． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在平面直角坐标系xOy中，点A在x轴的正半轴上，点B、C在第一象限，且四边形OABC是平行四边形，OC=2
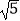，sin∠AOC= 
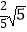，反比例函数y= 
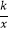的图象经过点C以及边AB的中点D． 
（1）求这个反比例函数的解析式；
（2）四边形OABC的面积．
相关试题
