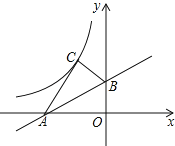
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=![]() (k≠0)上,则k的值为( )
(k≠0)上,则k的值为( )
A.4 B.﹣2 C.![]() D.﹣
D.﹣![]()
参考答案:
【答案】D
【解析】
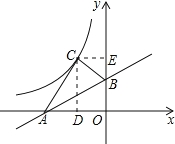
试题分析:设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,由折叠的性质易得∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,用锐角三角函数的定义得CD,CE,得点C的坐标,易得k.
解:设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,
∵将△ABO沿直线AB翻折,
∴∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,
∴CD=y=ACsin60°=2×![]() =
=![]() ,
,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD=30°,
∵BC=BO=AOtan30°=2×![]() =
=![]() ,
,
CE=x=BCcos30°=![]() =1,
=1,
∵点C恰好落在双曲线y=![]() (k≠0)上,
(k≠0)上,
∴k=xy=﹣1×![]() =﹣
=﹣![]() ,
,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣1)(x+3)=x2+px﹣3,则p=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
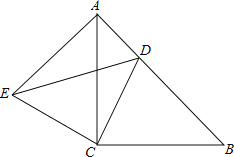
(1)试说明:∠EAC=∠B;
(2)若AD=10,BD=24,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:
 ≈1.732)
≈1.732)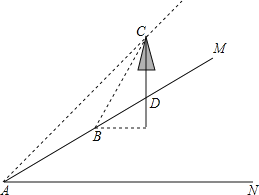
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
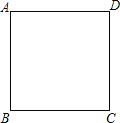
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3x=4,9y=7,则3x+2y的值为_________.
相关试题

