搜索
【题目】如图，
，点D在边BC上
与B、C不重合
，四边形ADEF为正方形，过点F作
，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：
；
：
：2；
；
其中正确的结论的个数是
A. 0 B. 1 C. 2 D. 3
参考答案：
【答案】D
【解析】分析：由正方形的性质得出
，证出
，由AAS证明
≌
，得出
，①正确；
证明四边形CBFG是矩形，得出
②正确；
由等腰直角三角形的性质和矩形的性质得出
，③正确；
详解：∵四边形ADEF为正方形，
∴
∴
∵FG⊥CA，
∴
∴∠CAD=∠AFG，
在△FGA和△ACD中,
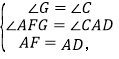
∴△FGA≌△ACD(AAS)，
∴AC=FG，①正确；
∵BC=AC，
∴FG=BC，
∵
，FG⊥CA，
∴FG∥BC，
∴四边形CBFG是矩形，
∴
②正确；
∵
∴
③正确；
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，A，B在数轴上对应的数分别用a，b表示，且（
ab+100）2+|a﹣20|=0，P是数轴上的一个动点．（1）在数轴上标出A、B的位置，并求出A、B之间的距离．
（2）已知线段OB上有点C且|BC|=6，当数轴上有点P满足PB=2PC时，求P点对应的数．
（3）动点P从原点开始第一次向左移动1个单位长度，第二次向右移动3个单位长度，第三次向左移动5个单位长度第四次向右移动7个单位长度，…．点P能移动到与A或B重合的位置吗？若都不能，请直接回答．若能，请直接指出，第几次移动与哪一点重合？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△OAB中，O为坐标原点，横、纵轴的单位长度相同，A、B的坐标分别为(8，6)，(16，0)，点P沿OA边从点O开始向终点A运动，速度每秒1个单位，点Q沿BO边从B点开始向终点O运动，速度每秒2个单位，如果P、Q同时出发，用t(秒)表示移动时间，当这两点中有一点到达自己的终点时，另一点也停止运动。求：
（1）几秒时PQ∥AB.
（2）设△OPQ的面积为y，求y与t的函数关系式.
（3）△OPQ与△OAB能否相似?若能，求出点P的坐标，若不能，试说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，下列四组条件中，能判定ABCD是正方形的有
①AB=BC，∠BAD=90°；
；
；
．
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各式
（1）﹣（﹣5）﹣（+7）
（2）|﹣5﹣8|+24÷（﹣3）
（3）﹣0.25÷（﹣
）×（1﹣
）（4）36×（
）（5）1÷[
﹣（﹣1+1
）]×4（6）23﹣（1﹣0.5）×
×[2﹣（﹣3）2] -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3 ， …组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒
个单位长度，则第2015秒时，点P的坐标是（ ）
A.（2014，0）
B.（2015，﹣1）
C.（2015，1）
D.（2016，0） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：点M、P、N、Q依次是正方形ABCD的边AB、BC、CD、DA上一点（不与正方形的顶点重合），给出如下结论：
①MN⊥PQ，则MN=PQ；
②MN=PQ，则MN⊥PQ；
③△AMQ≌△CNP，则△BMP≌△DNQ；
④△AMQ∽△CNP，则△BMP∽△DNQ
其中所有正确的结论的序号是 ．
相关试题
