【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)当t=1时,正方形EFGH的边长是 . 当t=3时,正方形EFGH的边长是 .
(2)当0<t≤2时,求S与t的函数关系式;
(3)直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少? 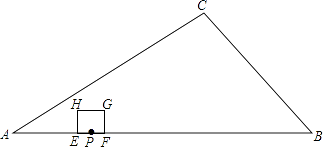
参考答案:
【答案】
(1)2;4
(2)解:
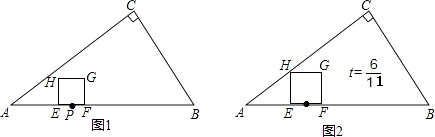 ,
,
如图1,EP=FP=t,HE=EF=2t,
如图2,EP=FP=t,HE=EF=2t,
AE=AP﹣EP=2﹣t,
由 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() 得t=
得t= ![]() ,
,
故S重叠面积=S正方形=(2t)2=4t2(0<t≤ ![]() ),
),
如图4,AE=AP﹣EP=2﹣t,
LE= ![]() AE=
AE= ![]() ,
,
HL=HE﹣LE=2t﹣ ![]() (2﹣t),
(2﹣t),
HM= ![]() HL=
HL= ![]() [2t﹣
[2t﹣ ![]() (2﹣t)],
(2﹣t)],
由HG= ![]() HL,即2t=
HL,即2t= ![]() [2t﹣
[2t﹣ ![]() (2﹣t)]
(2﹣t)]
解得:t= ![]() ,
,
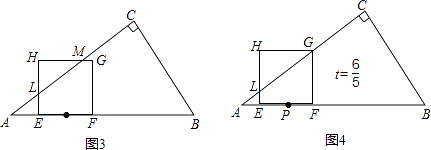
如图3,AE=AP﹣EP=2﹣t,
LE= ![]() AE=
AE= ![]() ,
,
HL=HE﹣LE=2t﹣ ![]() (2﹣t),
(2﹣t),
HM= ![]() HL=
HL= ![]() [2t﹣
[2t﹣ ![]() (2﹣t)],
(2﹣t)],
S重叠面积=S正方形﹣S△HLM=EF2﹣ ![]() HL×HM=﹣
HL×HM=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() (
( ![]() <t≤
<t≤ ![]() );
);
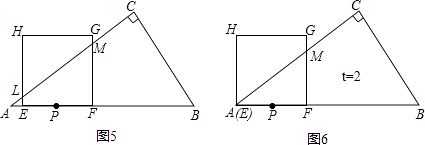
如图5,AE=AP﹣EP=2﹣t,LE= ![]() AE=
AE= ![]() (2﹣t),MF=
(2﹣t),MF= ![]() AF=
AF= ![]() (2+t),
(2+t),
S重叠面积=S梯形LEFM= ![]() (EL+MF)×EF=3t(
(EL+MF)×EF=3t( ![]() <t≤2)
<t≤2)
(3)解:由(2)知:当0<t≤ ![]() 时,
时,
S与t的函数关系式是S=2t×2t=4t2= ![]() ;
;
当 ![]() <t≤
<t≤ ![]() 时,
时,
S与t的函数关系式是:
S=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() =
= ![]() ;
;
当 ![]() <t≤2时;
<t≤2时;
S与t的函数关系式是:
S=3t=6;
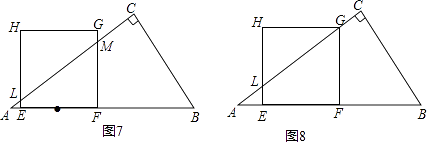
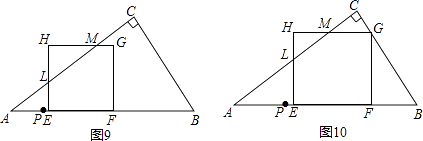
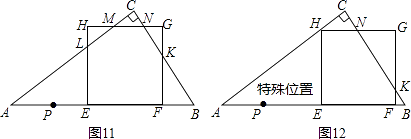
当t>2时,观察正方形与三角形的重叠面积随t值变化情况,容易得到只有当 ![]() ≤t≤
≤t≤ ![]() 时,S才有可能取到最大值.如图7,图8,图9,图10,图11,图12,
时,S才有可能取到最大值.如图7,图8,图9,图10,图11,图12,
显然,图10,图12是图11的特殊情况,只要算出图11的重叠面积关于t的函数关系式,即可得出在图11中,
由PA+AE=t,得AE=t﹣2,FB=AB﹣AE﹣EF=10﹣(t﹣2)﹣4=8﹣t,
由LE= ![]() E=
E= ![]() (t﹣2),HL=HE﹣LE=4﹣
(t﹣2),HL=HE﹣LE=4﹣ ![]() (t﹣2),HM=
(t﹣2),HM= ![]() HL=
HL= ![]() [4﹣
[4﹣ ![]() (t﹣2)]
(t﹣2)]
得S△HLM= ![]() HL×HM=
HL×HM= ![]() [4﹣
[4﹣ ![]() (t﹣2)]×
(t﹣2)]× ![]() [4﹣
[4﹣ ![]() (t﹣2)]
(t﹣2)]
由FB=AB﹣AE﹣EF=10﹣(t﹣2)﹣4=8﹣t,则FK= ![]() (8﹣t),GK=GF﹣KF=4﹣
(8﹣t),GK=GF﹣KF=4﹣ ![]() (8﹣t),
(8﹣t),
由NG= ![]() GK=
GK= ![]() [4﹣
[4﹣ ![]() (8﹣t)],
(8﹣t)],
则S△NGK= ![]() GK×NG=
GK×NG= ![]() [4﹣
[4﹣ ![]() (8﹣t)]×
(8﹣t)]× ![]() [4﹣
[4﹣ ![]() (8﹣t)],
(8﹣t)],
S重叠面积=16﹣S△NCK﹣S△HLM═﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() ,
,
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]()
∴综上所述,当t= ![]() 时S有最大值,为
时S有最大值,为 ![]() .
.
由图形知,在整个过程中,S取得最大值只会在图11中产生,故当t= ![]() 时S有最大值,为
时S有最大值,为
【解析】解:(1)当时t=1时,则PE=1,PF=1, ∴正方形EFGH的边长是2;
当t=3时,PE=1,PF=3,
∴正方形EFGH的边长是4.
所以答案是:2,4;
【考点精析】根据题目的已知条件,利用二次函数的最值和勾股定理的概念的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.

(1)直线BD是否与⊙O相切?为什么?
(2)连接CD,若CD=5,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.

(1)求此二次函数关系式和点B的坐标;
(2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1 , 时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式:
 请你完成:
请你完成: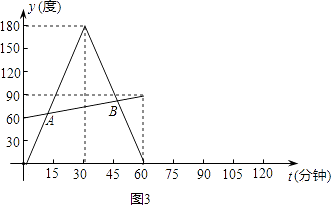

(1)求出图3中y2与t的函数关系式;
(2)直接写出A、B两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一个小时,请你在题图3中补全图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的顶点分别为A(1,1)、B(1,﹣1)、C(﹣1,﹣1)、D(﹣1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1 , 作P1关于点B的对称点P2 , 作点P2关于点C的对称点P3 , 作P3关于点D的对称点P4 , 作点P4关于点A的对称点P5 , 作P5关于点B的对称点P6┅,按如此操作下去,则点P2011的坐标为( )

A.(0,2)
B.(2,0)
C.(0,﹣2)
D.(﹣2,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 ,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2 , 则y1、y2必须满足( )
,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2 , 则y1、y2必须满足( )
A.y1>0、y2>0
B.y1<0、y2<0
C.y1<0、y2>0
D.y1>0、y2<0 -
科目: 来源: 题型:
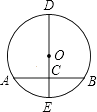
查看答案和解析>>【题目】如图,DE是⊙O的直径,弦AB⊥CD,垂足为C,若AB=6,CE=1,则OC= , CD= .
相关试题

