【题目】小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1 , 时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式: ![]() 请你完成:
请你完成: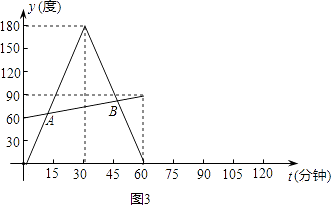

(1)求出图3中y2与t的函数关系式;
(2)直接写出A、B两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一个小时,请你在题图3中补全图象.
参考答案:
【答案】
(1)解:设y2与t的函数关系式为y2=kt+b,再把(0,60),(60,90)代入得: ![]() ,解得
,解得 ![]() ,
,
则解析式是:y=0.5t+60.
故y2与t的函数关系式为y2=0.5t+60
(2)解:A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() );
);
当0≤t≤30时, ![]() ,解得
,解得  ;
;
当30<t≤60时, ![]() ,解得
,解得 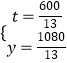 ,
,
故A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() );
);
A表示时针与分针第一次重合的情况,B表示是经过 ![]() 分钟时针与分针关于OP成轴对称且与OP的夹角为
分钟时针与分针关于OP成轴对称且与OP的夹角为 ![]()
(3)解:

【解析】(1)设y2与t的函数关系式为y2=kt+b,再把(0,60),(60,90)代入此函数关系式即可求出k、b的值,进而得出结论;(2)求出两个函数的交点坐标即可;(3)分针会再转一圈,与第一个小时的情况相同,是一个循环,而时针OP的夹角增大的速度与第一个小时相同,即函数图象向右延伸.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阳光中学九(1)班同学在一次综合实践活动中,对本县居民参加“全民医保“情况进行了调查.同学们利用节假日随机调查了2000人,对调查结果进行了系统分析.绘制出两幅不完整的统计图:

(注:图中A表示“城镇职工基本医疗保险”,B表示“城镇居民基本医疗保险”;C表示“新型农村合作医疗”;D表示其他情况)
(1)补全条形统计图;
(2)在本次调查中,B类人数占被调查人数的百分比为
(3)据了解,国家对B类人员每人每年补助155元,已知该县人口约80万人,请估计该县B类人员每年享受国家补助共多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.

(1)直线BD是否与⊙O相切?为什么?
(2)连接CD,若CD=5,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.

(1)求此二次函数关系式和点B的坐标;
(2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)当t=1时,正方形EFGH的边长是 . 当t=3时,正方形EFGH的边长是 .
(2)当0<t≤2时,求S与t的函数关系式;
(3)直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?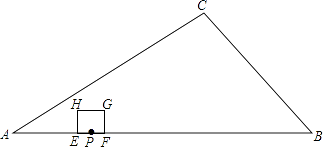
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的顶点分别为A(1,1)、B(1,﹣1)、C(﹣1,﹣1)、D(﹣1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1 , 作P1关于点B的对称点P2 , 作点P2关于点C的对称点P3 , 作P3关于点D的对称点P4 , 作点P4关于点A的对称点P5 , 作P5关于点B的对称点P6┅,按如此操作下去,则点P2011的坐标为( )

A.(0,2)
B.(2,0)
C.(0,﹣2)
D.(﹣2,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 ,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2 , 则y1、y2必须满足( )
,当自变量x取m时对应的值大于0,当自变量x分别取m﹣1、m+1时对应的函数值为y1、y2 , 则y1、y2必须满足( )
A.y1>0、y2>0
B.y1<0、y2<0
C.y1<0、y2>0
D.y1>0、y2<0
相关试题

