【题目】如图,过ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的AEMG的面积S1与HCFM的面积S2的大小关系是( )
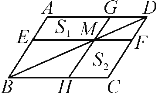
A. S1>S2 B. S1<S2 C. S1=S2 D. 2S1=S2
参考答案:
【答案】C
【解析】
根据平行四边形的性质和判定得出平行四边形HBEM、GMFD,证△ABD≌△CDB,得出△ABD和△CDB的面积相等;同理得出△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,相减即可求出答案.
∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中;
∵ ,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2﹣2x , 其对称轴与两抛物线所围成的阴影部分的面积是 .
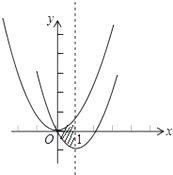
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,客轮沿折线A—B—C从A点出发经过B点再到C点匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮的速度是货轮速度的2倍.
(1)选择题:两船相遇之处E点( )
A.在线段AB上
B.在线段BC上
C.可能在线段AB上,也可能在线段BC上
(2)货轮从出发到两船相遇共航行了多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC和∠BOC互补,则弦BC的长度为 .
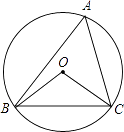
-
科目: 来源: 题型:
查看答案和解析>>【题目】一圆的半径是10cm,圆内的两条平行弦长分别为12cm和16cm,则这两条平行弦之间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连结OE.下列结论:
BC,连结OE.下列结论:①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=
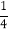 BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)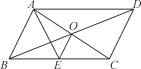
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
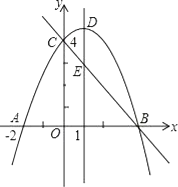
(1)求抛物线的解析式;
(2)若直线BC的函数解析式为y’=kx+b,求当满足y<y’时,自变量x的取值范围.
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
相关试题

