【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.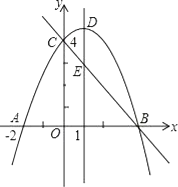
(1)求抛物线的解析式;
(2)若直线BC的函数解析式为y’=kx+b,求当满足y<y’时,自变量x的取值范围.
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
参考答案:
【答案】
(1)解:∵抛物线y=ax2+bx+c(a≠0)过点C(0,4),
∴c=4 ①.
∵对称轴x=- ![]() =1,
=1,
∴b=-2a ②.
∵抛物线过点A(-2,0),
∴0=4a-2b+c ③,
由①②③解得,a=- ![]() ,b=1,c=4,
,b=1,c=4,
∴抛物线的解析式为y=- ![]() x2+x+4;
x2+x+4;
(2)解:∵A(﹣2,0),对称轴x=1,
∴B(4,0)
根据图像,得x<0 或x>4时,y
(3)解:已知DE∥PQ,当DE=PQ时,以D、E、P、Q为顶点的四边形是平行四边形,
设点P的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣ ![]() m2+m+4),
m2+m+4),
∴|﹣m+4+ ![]() m2﹣m﹣4|=DE=
m2﹣m﹣4|=DE= ![]() ,
,

∴m=1,m=3,m= ![]() ,m=
,m= ![]()
当m=1时,线段PQ与DE重合,舍去.
∴P1(3,1),
P2( ![]() ,
, ![]() ),
),
P3( ![]() ,
, ![]() ).
).
【解析】(1)方法一、根据点C的坐标可求得c=4,根据对称轴x=1,得出b=-2a ,将点A的坐标代入解析式得出0=4a-2b+c ,联立求解,即可求出函数解析式。方法二、根据二次函数的对称性,由点A的坐标及抛物线的对称轴x=1,求出点B的坐标,然后设函数解析式为交点式,再将点C的坐标代入求出a的值,即可求出函数解析式。
(2)先求出点B的坐标,根据点A、B的坐标,观察函数图像要使y<y’时,就要观察抛物线低于直线BC的部分,即可求出结果。
(3)抓住已知条件平行于DE的一条动直线l,可知DE∥PQ,点P和点Q的横坐标相等,要证以D、E、P、Q为顶点的四边形是平行四边形,只需证得DE=PQ即可。先根据点P和点Q的横坐标相等,分别设出两点坐标,再根据DE=PQ建立方程,求解即可求得点P的坐标。
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的AEMG的面积S1与HCFM的面积S2的大小关系是( )
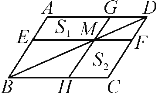
A. S1>S2 B. S1<S2 C. S1=S2 D. 2S1=S2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一圆的半径是10cm,圆内的两条平行弦长分别为12cm和16cm,则这两条平行弦之间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连结OE.下列结论:
BC,连结OE.下列结论:①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=
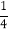 BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=
 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.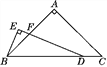
-
科目: 来源: 题型:
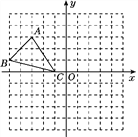
查看答案和解析>>【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A2的坐标为__________,点A2 019的坐标为__________;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为_______________.
相关试题

