【题目】如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
(1)当矩形EFPQ为正方形时,求正方形的边长;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线BC匀速向右运动(当矩形的顶点Q到达C点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.

参考答案:
【答案】(1)当矩形EFPQ为正方形时,边长为![]() ;(2)当x=
;(2)当x=![]() 时,矩形EFPQ的面积最大,最大面积为5;(3)当0≤t≤
时,矩形EFPQ的面积最大,最大面积为5;(3)当0≤t≤![]() 时,S =5-2t2;当
时,S =5-2t2;当![]() <t<2.5时,S=
<t<2.5时,S=![]() -2t;当2.5≤t≤3时,S=2t2-12t+18
-2t;当2.5≤t≤3时,S=2t2-12t+18
【解析】(1)由条件可得![]() ,即
,即![]() ,计算即可.
,计算即可.
(2)可利用![]() 用x表示出EH.表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
用x表示出EH.表示出矩形EFPQ的面积,利用二次函数可求得其最大值;
(3)分0≤t≤![]() ,
,![]() ,2.5≤t≤3三种情况进行讨论即可.
,2.5≤t≤3三种情况进行讨论即可.
(1)∵四边形EFPQ为矩形,
∴EF∥BC,
![]() ,
,
即![]() ,
,
解得![]()
∴当矩形EFPQ为正方形时,边长为![]() .
.
即当x为![]() 时,矩形EFPQ为正方形;
时,矩形EFPQ为正方形;
(2)∵∠B=45°,
∴![]() ,
,
∴![]()
∵EF∥BC,
∴△AEH∽△ABD,∴![]() ,
,
∵EF∥BC,∴△AFH∽△ACD,∴![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
已知EF=x,则EH=![]() .
.
∵∠B=45°,
∴![]() =4﹣
=4﹣![]() .
.
S矩形EFPQ![]()
∴当x=![]() 时,矩形EFPQ的面积最大,最大面积为5.
时,矩形EFPQ的面积最大,最大面积为5.
(3)如图①,当0≤t≤![]() 时
时

设EF交AC于M点,FP交AC于N点,
∵△MNF∽△CAD,
∴![]() ,
,
即![]() ,
,
∴FN=4t ,
∴S=5-![]() t·4t,
t·4t,
=5-2t2
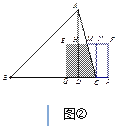
如图②,当![]() 时
时
设EF交AC于M点,过C作CN⊥EF于N点,
∵△CNM∽△ADC
∴![]() ,
,
即![]() ,
,
∴MN=![]() ,
,
∴FN=t-![]() ,
,
∴S=5-![]() (t-
(t-![]() +t),
+t),
=![]() -2t ,
-2t ,
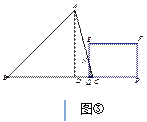
如图③,当2.5≤t≤3时
设EQ交AC于N点,
∵△CQN∽△CDA
∴![]() ,
,
![]() ,
,
∴NQ=12-4t,
∴S=![]() (3-t)(12-4t)
(3-t)(12-4t)
=2t2-12t+18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
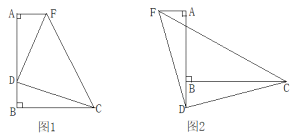
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
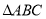 中,
中,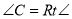 ,
, ,
, .若动点
.若动点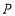 从点
从点 开始,沿
开始,沿 的路径运动,且速度为每秒
的路径运动,且速度为每秒 ,设运动的时间为
,设运动的时间为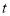 秒,当
秒,当 ______时,
______时, 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.
(1)求打折前每本笔记本的售价是多少元?
(2)由于考虑学生的需求不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不低于360元,且不超过365元,问有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF的长是( )
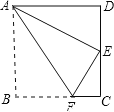
A. 7.5 B. 8 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为提高学生的计算能力,我县某学校八年级在元旦之前组织了一次数学速算比赛。速算规则如下:速算试题形式为计算题,共20道题,答对一题得5分,不答或错一题倒扣1分.小明代表班级参加了这次比赛,请解决下列问题:
(1)如果小明最后得分为70分,那么他计算对了多少道题?
(2)小明的最后得分可能为90分吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(观察思考):
如图,线段
 上有两个点
上有两个点 ,图中共有_________条线段;
,图中共有_________条线段;
(2)(模型构建):
如果线段上有
 个点(包括线段的两个端点),则该线段上共有___________条线段;
个点(包括线段的两个端点),则该线段上共有___________条线段;(3)(拓展应用):
某班8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行__________场比赛.
相关试题

