【题目】(1)(观察思考):
如图,线段![]() 上有两个点
上有两个点![]() ,图中共有_________条线段;
,图中共有_________条线段;
![]()
(2)(模型构建):
如果线段上有![]() 个点(包括线段的两个端点),则该线段上共有___________条线段;
个点(包括线段的两个端点),则该线段上共有___________条线段;
(3)(拓展应用):
某班8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行__________场比赛.
参考答案:
【答案】解:(1)6;(2)![]() ;(3)28
;(3)28
【解析】
(1)从左向右依次固定一个端点A、D、C找出线段,再求和即可;
(2)根据数线段的特点列出式子并化简,就能解答本问;
(3)将实际问题转化成(2)的模型,借助(2)的结论解答.
(1)∵以点A为左端点向右的线段有:线段AB、AC、AD,
以点D为左端点向右的线段有线段DC、DB,
以点C为左端点的线段有线段CB,
∴共有3+2+1=6条线段;
故答案为:6
(2)![]() .理由如下:
.理由如下:
设线段上有m个点,该线段上共有线段x条,
则x=(m-1)+(m-2)+(m-3)+…+3+2+1①
∴倒序排列有x=1+2+3+…+(m-3)+(m-2)+(m-1)②
+②得:2x=m(m-1),
![]() ,
,
故有![]() 条线段;
条线段;
故答案为: ![]()
(3)把8位同学看作直线上的8个点,每两位同学之间的一场象棋比赛看作为一条线段,
直线上8个点所构成的线段条数就等于象棋比赛的场数,
因此一共要进行![]() (场)
(场)
故答案为:28
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
(1)当矩形EFPQ为正方形时,求正方形的边长;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线BC匀速向右运动(当矩形的顶点Q到达C点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.

-
科目: 来源: 题型:
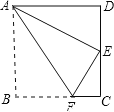
查看答案和解析>>【题目】如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF的长是( )
A. 7.5 B. 8 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为提高学生的计算能力,我县某学校八年级在元旦之前组织了一次数学速算比赛。速算规则如下:速算试题形式为计算题,共20道题,答对一题得5分,不答或错一题倒扣1分.小明代表班级参加了这次比赛,请解决下列问题:
(1)如果小明最后得分为70分,那么他计算对了多少道题?
(2)小明的最后得分可能为90分吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步推动我县校园足球运动的发展,提高全县中小学生足球竞技体育水平,选拔和培养优秀足球后备人才,增强青少年体质,进一步营造全社会关注青少年足球运动的氛围,汶上县第五届“县长杯”校园足球比赛于2019年11月9日—11月24日成功举办.我县县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格分别是多少;
(2)若城区四校联合购买100套队服和
 个足球,请用含
个足球,请用含 的式子分别表示出到甲商场和乙商场购买装备所花的费用;
的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)在(2)的条件下,若
 ,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?
,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的平行线交
的平行线交 的延长线于
的延长线于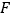 ,且
,且 ,连结
,连结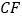 .
.(1)求证:
 是
是 的中点;
的中点;(2)如果
 ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】灌云教育局为了解今年九年级学生体育测试情况,随机抽查了部分学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
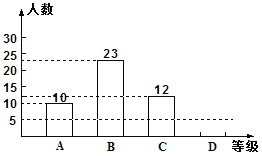
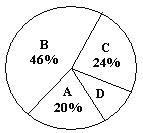
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)样本中D级的学生人数占全班学生人数的百分比是_____________;
(3)扇形统计图中A级所在的扇形的圆心角度数是_____________;
(4)若该县九年级有8000名学生,请你用此样本估计体育测试中A级和B级的学生人数之和.
相关试题

