【题目】如图,F是菱形ABCD的边AD的中点,AC与BF相交于E,![]() 于G,已知
于G,已知![]() ,则下列结论:
,则下列结论:![]() ;
;![]() ;
;![]() :
:![]() 其中正确的结论是
其中正确的结论是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
证![]() =
=![]() ,可得
,可得![]() 易证△AEF≌△AEG(SAS),所以,∠AFE=∠AGE,所以,
易证△AEF≌△AEG(SAS),所以,∠AFE=∠AGE,所以,![]() ;由
;由![]() =
=![]() ,可证
,可证![]() =
=![]() ,连接BD,易证△ABF≌△BAO,可得,BF=AO,所以,AC=2BF;同理,可证△BOE≌△BGF,可得,OE=EG,所以,CE=CO+OE=BF+EG.
,连接BD,易证△ABF≌△BAO,可得,BF=AO,所以,AC=2BF;同理,可证△BOE≌△BGF,可得,OE=EG,所以,CE=CO+OE=BF+EG.
因为,四边形ABCD是菱形,
所以,![]() ,AB=AD=CD=BC,
,AB=AD=CD=BC,
所以,![]() =
=![]() ,
,
所以,![]()
因为![]() ,
,
所以,![]() =
=![]() ,
,
又因为![]() ,
,
所以,![]() ,AG=
,AG=![]() ,
,
又因为F是菱形ABCD的边AD的中点,
所以,AF=![]() ,
,
所以,AF=AG,
所以,易证△AEF≌△AEG(SAS),
所以,∠AFE=∠AGE,
所以,![]() ,
,
所以,由![]() =
=![]() ,
,
可证![]() =
=![]() ,
,
连接BD,
易证△ABF≌△BAO,
所以,BF=AO,
所以,AC=2BF,
同理,可证△BOE≌△BGF,
所以,OE=EG,
所以,CE=CO+OE=BF+EG,
综合上述,![]() 正确
正确

故选:A
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于O,EF经过点O,分别交AD,BC于E,F,已知ABCD的面积是
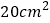 ,则图中阴影部分的面积是
,则图中阴影部分的面积是

A. 12
 B. 10
B. 10 C.
C.  D.
D. 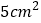
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第一个等式:a1=
 =
= -
-
第二个等式:a2=
 =
= -
-
第三个等式:a3=
 =
= -
-
第四个等式:a4=
 =
= -
-
按上述规律,回答下列问题:
(1)请写出第六个等式:a6=_____=_____;
(2)用含n的代数式表示第n个等式:an=_____=_____;
(3)a1+a2+a3+a4+a5+a6=_____(得出最简结果);
(4)计算:a1+a2+…+an.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:
 ;
;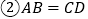 ;
;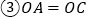 ;
;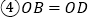 ,从中任选两个条件,能使四边形ABCD为平行四边形的选法有
,从中任选两个条件,能使四边形ABCD为平行四边形的选法有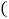
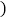
A. 2种 B. 3种 C. 4种 D. 5种
-
科目: 来源: 题型:
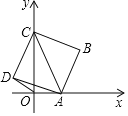
查看答案和解析>>【题目】如图,点A是x轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是
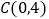 ,设点A的坐标为
,设点A的坐标为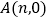 .
. 当
当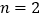 时,正方形ABCD的边长
时,正方形ABCD的边长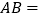 ______.
______.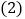 连结OD,当
连结OD,当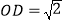 时,
时,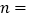 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m
0<m≤100
100<m≤200
m>200
收费标准(元/人)
90
85
75
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某学校有一块长为30米,宽为10米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道.
 若设计人行通道的宽度为2米,那么修建的两块矩形绿地的面积共为多少平方米?
若设计人行通道的宽度为2米,那么修建的两块矩形绿地的面积共为多少平方米? 若要修建的两块矩形绿地的面积共为216平方米,求人行通道的宽度.
若要修建的两块矩形绿地的面积共为216平方米,求人行通道的宽度.
相关试题

