【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:

(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
参考答案:
【答案】(1)0;(2)图见解析;(3)答案不唯一,合理即可;(4)①3,3;②2;③-1<a<0.
【解析】
试题分析:(1)观察表格,根据对称性即可得m=0;(2)根据表格描点,画出图象即可;(3)观察图象,写出函数的两条性质即可,可从函数的最值,增减性,图象的对称性等方面阐述,答案不唯一,合理即可;(4)①观察函数图像可得函数图像与![]() 轴有3个交点,所以对应方程
轴有3个交点,所以对应方程![]() 有3个实数根;②由图象可知,函数
有3个实数根;②由图象可知,函数![]() 图像与直线y=2有两个交点,所以方程有2个实数根;③方程
图像与直线y=2有两个交点,所以方程有2个实数根;③方程![]() 有4个实数根,说明函数
有4个实数根,说明函数![]() 的图象与直线y=a有4个交点,由此可得
的图象与直线y=a有4个交点,由此可得![]() 的取值范围是-1<a<0.
的取值范围是-1<a<0.
试题解析:(1)0;
(2)(正确补全图象);
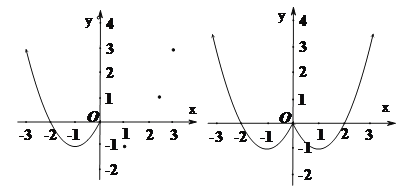
(3)(可从函数的最值,增减性,图象的对称性等方面阐述,答案不唯一,合理即可);
(4)①3,3;②2;③-1<a<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠A和∠B是同旁内角,∠A=30°,则∠B的度数( )
A. 30° B. 150° C. 30°或150° D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.7a+a=7a2
B.5y﹣3y=2
C.3x2y﹣2yx2=x2y
D.3a+2b=5ab -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,E为边CD的中点,联结AE并延长,交边BC的延长线于点F.
(1)求证:四边形ACFD是平行四边形;
(2)如果∠B+∠AFB=90°,求证:四边形ACFD是菱形.
-
科目: 来源: 题型:
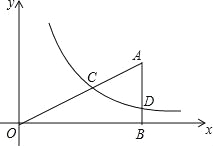
查看答案和解析>>【题目】(2016宁夏第24题)如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2
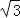 ,反比例函数y=
,反比例函数y=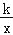 (x>0)的图象经过OA的中点C,交AB于点D.
(x>0)的图象经过OA的中点C,交AB于点D.(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的一个角为80°,则它的顶角的度数是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北省荆州市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.

问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线
 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
相关试题

