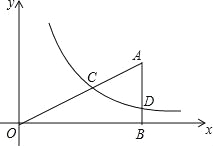
【题目】(2016宁夏第24题)如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2![]() ,反比例函数y=
,反比例函数y=![]() (x>0)的图象经过OA的中点C,交AB于点D.
(x>0)的图象经过OA的中点C,交AB于点D.
(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
参考答案:
【答案】(1)、y=![]() ;(2)、
;(2)、![]()
【解析】
试题分析:(1)、解直角三角形求得AB,作CE⊥OB于E,根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标,然后根据待定系数法即可求得反比例函数的解析式;(2)、求得D的坐标,进而求得AD的长,得出△ACD的面积,然后根据S四边形CDBO=S△AOB﹣S△ACD即可求得.
试题解析:(1)、∵∠ABO=90°,∠AOB=30°,OB=2![]() , ∴AB=
, ∴AB=![]() OB=2, 作CE⊥OB于E,
OB=2, 作CE⊥OB于E,
∵∠ABO=90°, ∴CE∥AB, ∴OC=AC, ∴OE=BE=![]() OB=
OB=![]() ,CE=
,CE=![]() AB=1, ∴C(
AB=1, ∴C(![]() ,1),
,1),
∵反比例函数y=![]() (x>0)的图象经过OA的中点C, ∴1=
(x>0)的图象经过OA的中点C, ∴1=![]() , ∴k=
, ∴k=![]() ,
,
∴反比例函数的关系式为y=![]() ;
;
(2)、∵OB=2![]() , ∴D的横坐标为2
, ∴D的横坐标为2![]() , 代入y=
, 代入y=![]() 得,y=
得,y=![]() , ∴D(2
, ∴D(2![]() ,
,![]() ), ∴BD=
), ∴BD=![]() ,
,
∵AB=2, ∴AD=![]() , ∴S△ACD=
, ∴S△ACD=![]() ADBE=
ADBE=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴S四边形CDBO=S△AOB﹣S△ACD=![]() OBAB﹣
OBAB﹣![]() =
=![]() ×2
×2![]() ×2﹣
×2﹣![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.7a+a=7a2
B.5y﹣3y=2
C.3x2y﹣2yx2=x2y
D.3a+2b=5ab -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,E为边CD的中点,联结AE并延长,交边BC的延长线于点F.
(1)求证:四边形ACFD是平行四边形;
(2)如果∠B+∠AFB=90°,求证:四边形ACFD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数
 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.(1)自变量
 的取值范围是全体实数,
的取值范围是全体实数, 与
与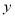 的几组对应值列表如下:
的几组对应值列表如下:
…
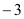
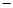
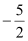
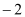
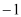
0
1
2
3
4
…
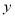
…
3
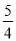
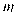
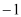
0
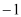
0
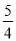
3
…
其中,
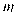 =____________.
=____________.(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:

(4)进一步探究函数图像发现:
①函数图像与
 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程 有___________个实数根;
有___________个实数根;②方程
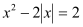 有___________个实数根;
有___________个实数根;③关于
 的方程
的方程 有4个实数根,
有4个实数根, 的取值范围是_______________________
的取值范围是_______________________ -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的一个角为80°,则它的顶角的度数是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北省荆州市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.

问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线
 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2a3=a6 B. 2a+3b=5ab C. a8÷a2=a6 D. (a2b)2=a4b
相关试题

