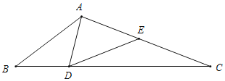
【题目】在△ABC中,∠B=30°,点D在BC边上,点E在AC边上,AD=BD,DE=CE,若△ADE为等腰三角形,则∠C的度数为_____°.
参考答案:
【答案】20或40.
【解析】
先根据三角形外角的性质,得出∠ADC=60°,则设∠C=∠EDC=α,进而得到∠ADE=60°α,∠AED=2α,∠DAE=120°α,最后根据△ADE为等腰三角形,进行分类讨论即可.
解:如图所示,∵AD=BD,∠B=30°,
∴∠BAD=30°,
∴∠ADC=60°,
∵DE=CE,
∴可设∠C=∠EDC=α,则∠ADE=60°﹣α,∠AED=2α,
根据三角形内角和定理可得,∠DAE=180°-(60°﹣α)-(2α)=120°﹣α,
分三种情况:
①当AE=AD时,则∠ADE=∠AED,即60°﹣α=2α,
解得α=20°;
②当DA=DE时,则∠DAE=∠AED,即120°﹣α=2α,
解得α=40°;
③当EA=ED时,则∠DAE=∠ADE,即120°﹣α=60°﹣α,方程无解,
综上所述,∠C的度数为20°或40°,
故答案为:20或40.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B分别在反比例函数y=
 (x>0),y=-
(x>0),y=- (x>0)的图象上且OA⊥OB,则
(x>0)的图象上且OA⊥OB,则 为( )
为( )
A.
 B.
B.  C.
C. 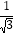 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
 (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y= (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
A. 10 B. 12 C. 14 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MPMD=MAME;③2CB2=CPCM.其中正确的是( )

A. ①②③ B. ① C. ①② D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,AB=AD,E是AC的中点.
(1)求证:∠EBD=∠EDB
(2)若∠BED=120°,试判断△BDC的形状.

相关试题

