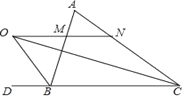
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,已知抛物线C1:y1=﹣x2+ax+b与抛物线C2:y2=2x2+4x+6为“友好抛物线”,抛物线C1与x轴交于点A、C,与y轴交于点B.
(1)求抛物线C1的表达式.
(2)若F(t,0)(﹣3<t<0)是x轴上的一点,过点F作x轴的垂线交抛物线与点P,交直线AB于点E,过点P作PD⊥AB于点D.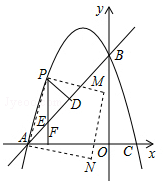
①是否存在点F,使PE+PD的值最大,若存在,请求出t的值;若不存在,请说明理由.
②连接PA,以AP为边作图示一侧的正方形APMN,随着点F的运动,正方形的大小、位置也随之改变.当正方形APMN中的边MN与y轴有且仅有一个交点时,求t的取值范围.
参考答案:
【答案】
(1)
解:由y2=2x2+4x+6=2(x+1)2+4,可知顶点坐标为(﹣1,4),
∵知抛物线C1:y1=﹣x2+ax+b与抛物线C2:y2=2x2+4x+6为“友好抛物线”,
∴顶点相同,抛物线C1的解析式为y1=﹣(x+1)2+4,
即y1=﹣x2﹣2x+3
(2)
解:①由题意易知A(﹣3,0),B(0,3),
∴OA=OB=3,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°﹣45°=45°,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD越大,PE+PD的值越大,
易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立 ![]() ,
,
消掉y得,x2+3x+m﹣3=0,
当△=32﹣4×1×(m﹣3)=0,
即m= ![]() 时,直线与抛物线只有一个交点,PD最长,
时,直线与抛物线只有一个交点,PD最长,
此时x=﹣ ![]() ,y=﹣
,y=﹣ ![]() +
+ ![]() =
= ![]() ,
,
∴点P(﹣ ![]() ,
, ![]() )时,PD+PE的值最大,
)时,PD+PE的值最大,
此时t=﹣ ![]() .
.
②抛物线y=﹣x2﹣2x+3的对称轴为直线x=﹣ ![]() =﹣1,
=﹣1,
(i)如图1,当点M在y轴上时,过点P作PQ⊥y轴于Q,
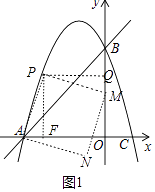
在正方形APMN中,AP=PM,∠APM=90°,
∴∠APF+∠FPM=90°,∠QPM+∠FPM=90°,
∴∠APF=∠QPM,
∵在△APF和△MPQ中,
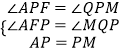 ,
,
∴△APF≌△MPQ(AAS),
∴PF=PQ,
∵点P的横坐标为t(t<0),则PQ=﹣t,
即PF=﹣t,
∴点P的坐标为(t,﹣t),
∵点P在抛物线y=﹣x2﹣2x+3上,
∴﹣t2﹣2t+3=﹣t,
整理得,t2+t﹣3=0,
解得t1= ![]() (舍去),t2=
(舍去),t2= ![]() ,
,
(ii)如图2,点N在y轴上时,
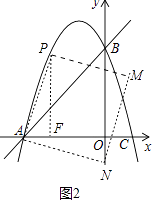
∵∠PAF+∠FPA=90°,∠PAF+∠QAN=90°,
∴∠FPA=∠QAN,
又∵∠PFA=∠AQN=90°,PA=AN,
∴△APF≌△NAO,
∴PF=AO,
则点P坐标为P(t,3),
则有﹣t2﹣2t+3=3,解得x=﹣2或0,
观察图象可知,当正方形APMN中的边MN与y轴有且仅有一个交点时,t的取值范围为 ![]() ≤t≤﹣2
≤t≤﹣2
【解析】(1)求出抛物线C1的顶点坐标即可解决问题;(2)①首先证明△PDE是等腰直角三角形,可知PD越大,PE+PD的值越大,易得直线AB的解析式为y=x+3,设与AB平行的直线解析式为y=x+m,联立 ![]() ,消掉y得,x2+3x+m﹣3=0,当△=32﹣4×1×(m﹣3)=0,即m=
,消掉y得,x2+3x+m﹣3=0,当△=32﹣4×1×(m﹣3)=0,即m= ![]() 时,直线与抛物线只有一个交点,PD最长,由此即可解决问题;②分两种情形(i)如图1中,当点M在y轴上时,(ii)如图2,点N在y轴上时,分别求解即可;
时,直线与抛物线只有一个交点,PD最长,由此即可解决问题;②分两种情形(i)如图1中,当点M在y轴上时,(ii)如图2,点N在y轴上时,分别求解即可;
【考点精析】关于本题考查的等腰直角三角形和二次函数的图象,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=
 ∠COF.
∠COF. 
(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在长方形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则AB=________.
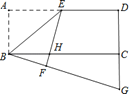
-
科目: 来源: 题型:
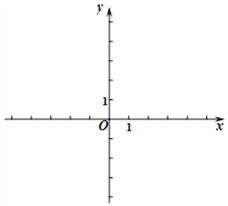
查看答案和解析>>【题目】已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交
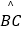 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( ) 
A.①②
B.①③
C.②③
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在直线AB上,AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
相关试题

