【题目】如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交 ![]() 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( ) 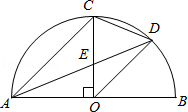
A.①②
B.①③
C.②③
D.①②③
参考答案:
【答案】B
【解析】解:∵OA=OD, ∴∠OAD=∠ODA,
∵AD为∠CAB的平分线,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴AC∥OD,故选项①正确;
∵OC⊥AB,OA=OC,
∴△AOC为等腰直角三角形,
∴∠DOB=∠COD=∠BAC=45°,
∵∠ADC与∠AOC都对 ![]() ,
,
∴∠ADC= ![]() ∠AOC=45°,
∠AOC=45°,
∴∠ADC=∠COD,又∠OCD=∠DCE,
∴△DCE∽△OCD,
∴ ![]() =
= ![]() ,即CD2=CEOC,
,即CD2=CEOC,
故选项③正确;
取 ![]() 的中点F,可得
的中点F,可得 ![]() =
= ![]() ,
,
∵ ![]() =2
=2 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AF=FC=CD,即AF+FC=2CD,
∵AF+FC>AC,
则2CD>AC,故选项②错误,
则正确的选项有:①③.
故选B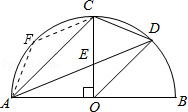
由OA=OD,利用等边对等角得到一对角相等,再由AD为角平分线得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行即可得到AC与OD平行,故选项①正确;由CO垂直于AB,OA=OC,得到三角形AOC为等腰直角三角形,得到∠CAB为45度,再由两直线平行同位角相等得到∠DOB为45度,即∠COD为45度,再由同弧所对的圆周角等于圆心角的一半得到∠ADC为45度,得到一对角相等,再由一对公共角,利用两对对应角相等的两三角形相似得到三角形CED与三角形OCD相似,由相似得比例可得出CD为CE与CO的比例中项,故选项③正确;取弧AC的中点F,得到弧AF与弧CF相等,再由弧AC=2弧CD,得到三条弧相等,利用等弧对等弦得到CF=AF=CD,即CF+AF=2CD,而CF+AF大于AC,可得出AC不等式2CD,故选项②错误.
-
科目: 来源: 题型:
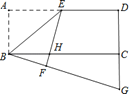
查看答案和解析>>【题目】已知如图,在长方形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则AB=________.
-
科目: 来源: 题型:
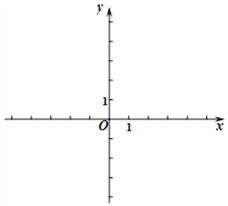
查看答案和解析>>【题目】已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,已知抛物线C1:y1=﹣x2+ax+b与抛物线C2:y2=2x2+4x+6为“友好抛物线”,抛物线C1与x轴交于点A、C,与y轴交于点B.

(1)求抛物线C1的表达式.
(2)若F(t,0)(﹣3<t<0)是x轴上的一点,过点F作x轴的垂线交抛物线与点P,交直线AB于点E,过点P作PD⊥AB于点D.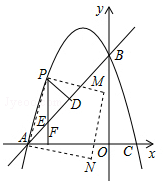
①是否存在点F,使PE+PD的值最大,若存在,请求出t的值;若不存在,请说明理由.
②连接PA,以AP为边作图示一侧的正方形APMN,随着点F的运动,正方形的大小、位置也随之改变.当正方形APMN中的边MN与y轴有且仅有一个交点时,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在直线AB上,AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长.
-
科目: 来源: 题型:
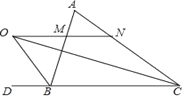
查看答案和解析>>【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )

A. ①② B. ②③ C. ①③ D. ①②③
相关试题

