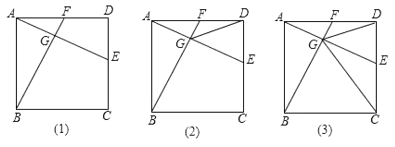
【题目】如图(1)在正方形![]() 中,点
中,点![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,作
,作![]() ,重足为
,重足为![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() 平分
平分![]() ,如图(2),求证:点
,如图(2),求证:点![]() 是
是![]() 中点:
中点:
(3)在(2)的条件下,连接![]() ,如图(3),求证:
,如图(3),求证:![]() .
.
参考答案:
【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
(1)证明△BAF≌△ADE(ASA)即可解决问题;
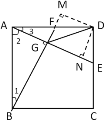
(2) 过点D作DM⊥GF,DN⊥GE,垂足分别为点M、N,先根据AAS证得△BAG≌△AND,推出AG=DN,再由角平分线的性质可知DM=DN,即DM=AG,再证△AFG≌△DFM,推出AF=DF=DE=![]() AD=
AD=![]() CD,即点E是CD的中点 ;
CD,即点E是CD的中点 ;
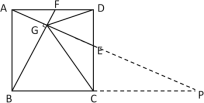
(3)延长AE,BC交于点P,由(2)知DE=CD,证得△ADE≌△PCE,推出AE=PE,再根据中位线判定定理即可得到CB=PC,利用直角三角形斜边中线的性质可证明CG=![]() BP=BC=CP ,即为所证 .
BP=BC=CP ,即为所证 .
(1)证明:在正方形ABCD中,AB=AD,∠BAD=∠D=90o
∴∠2+∠3=90o
又 ∵ BF⊥AE ∴∠1+∠2=90o ∴∠1=∠3
在△BAF与△ADE中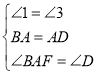
∴ △BAF≌△ADE
∴AF=DE

(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M、N,
由(1)得∠1=∠3 , ∠BGA=∠AND=90o AB=AD
∴ △BAG≌△ADN ∴AG=DN
又DG平分∠EGF,DM⊥GF,DN⊥GE
∴ DM=DN
∴ DM=AG
又∠AFG=∠DFM , ∠AGF=∠DMF
∴ △AFG≌△DFM
∴AF=DF=DE=![]() AD=
AD=![]() CD
CD
即点E是CD的中点.
(3)延长AE,BC交于点P,由(2)知DE=CE,
∵∠ADE=∠ECP=90o,∠DEA=∠CEP
∴ △ADE≌△PCE
∴AE=PE
又∵CE∥AB ∴ BC=PC
在Rt△BGP中,BC=PC
∴CG=![]() BP=BC
BP=BC
∴CG=CD
-
科目: 来源: 题型:
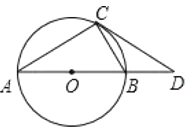
查看答案和解析>>【题目】如图所示,
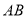 是
是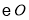 的直径,
的直径,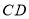 与
与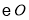 相切于点
相切于点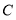 ,与
,与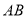 的延长线交于点
的延长线交于点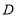 .
.
(1)求证:
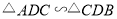 ;
;(2)若
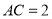 ,
,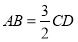 ,求
,求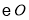 的半径.
的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
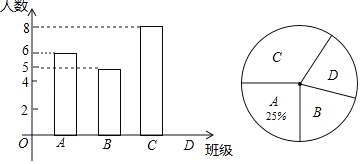
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
-
科目: 来源: 题型:
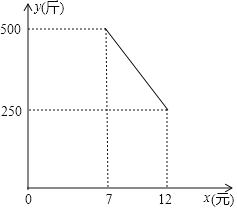
查看答案和解析>>【题目】某水果店每天的房租、人员工资等固定成本250元,水果进价是5元/斤,物价局规定售价不得高于12元/斤,也不得低于7元/斤,调查发现日均销量y(斤)与售价x(元)满足一次函数关系,图象如图.
(1)求日均销量y(斤)与销售单价x(元)之间的函数关系式,并写出自变量取值范围;
(2)设每天净利润为W元,那么定价多少时,可获得最大净利润?最大是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
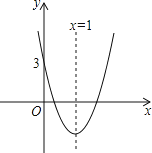
A. ②③④B. ①②③C. ②③D. ①④
-
科目: 来源: 题型:
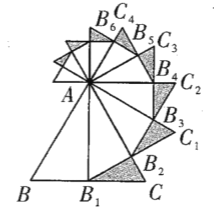
查看答案和解析>>【题目】如图,已知等边
 的边长是
的边长是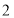 ,以
,以 边上的高
边上的高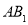 ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边 ;再以等边
;再以等边 的
的 边上的高
边上的高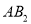 ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边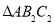 ,再以等边
,再以等边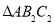 的
的 边上的高
边上的高 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边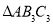 : ....记
: ....记 的面积为
的面积为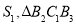 的面积为
的面积为 的面积为
的面积为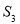 ,如此下去,则
,如此下去,则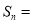 ___________
___________
相关试题

