【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
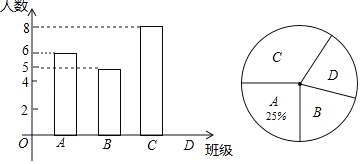
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
参考答案:
【答案】(1)5,120°;(2)见解析,![]() .
.
【解析】
(1)由A的人数和其所占的百分比即可求出总人数,由此即可求出D班满分人数,根据C班满分人数的百分比可求出其所对应扇形的圆心角的度数;
(2)列表得出所有等可能的情况数,找出刚好抽到一男一女的情况数,即可求出所求的概率.
解:(1)满分人数为6÷25%=24(人),
∴D班满分人数共24﹣6﹣5﹣8=5(人),
C班满分人数的扇形圆心角的度数=360°×![]() =120°,
=120°,
故答案为:5;120°;
(2)画树状图为:

或列表如下:
男 | 女1 | 女2 | 女3 | |
男 | ﹣﹣﹣ | (女,男) | (女,男) | (女,男) |
女1 | (男,女) | ﹣﹣﹣ | (女,女) | (女,女) |
女2 | (男,女) | (女,女) | ﹣﹣﹣ | (女,女) |
女3 | (男,女) | (女,女) | (女,女) | ﹣﹣﹣ |
∵共有12种等可能情况,1男1女有6种情况,设题中1男1女为事件A,
∴P(A)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,(k+1)2=k2+2k+1,变形得:(k+1)2﹣k2=2k+1,对上面的等式,依次令k=1,2,3,…得:
第1个等式:22﹣12=2×1+1
第2个等式:32﹣22=2×2+1
第3个等式:42﹣32=2×3+1
(1)按规律,写出第n个等式(用含n的等式表示):第n个等式 .
(2)记S1=1+2+3+…+n,将这n个等式两边分别相加,你能求出S1的公式吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“五一”期间,小明一家到某农庄采摘,在村口A处,小明接到农庄发来的定位,发现农庄C在自己的北偏东45°方向,于是沿河边笔直绿道l步行200米到达B处,此时定位显示农庄C在自己的北偏东30°方向,电话联系,得知农庄主已到农庄C正南方的桥头D处等待,请问还要沿绿道直走多少米才能到达桥头D处.(精确到1米,参考数据:
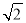 ≈1.414,
≈1.414,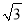 ≈1.732)
≈1.732)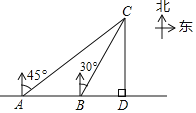
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
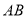 是
是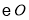 的直径,
的直径,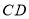 与
与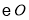 相切于点
相切于点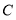 ,与
,与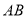 的延长线交于点
的延长线交于点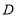 .
.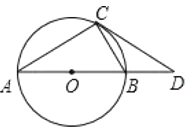
(1)求证:
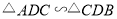 ;
;(2)若
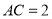 ,
,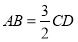 ,求
,求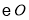 的半径.
的半径. -
科目: 来源: 题型:
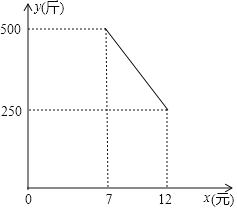
查看答案和解析>>【题目】某水果店每天的房租、人员工资等固定成本250元,水果进价是5元/斤,物价局规定售价不得高于12元/斤,也不得低于7元/斤,调查发现日均销量y(斤)与售价x(元)满足一次函数关系,图象如图.
(1)求日均销量y(斤)与销售单价x(元)之间的函数关系式,并写出自变量取值范围;
(2)设每天净利润为W元,那么定价多少时,可获得最大净利润?最大是多少?
-
科目: 来源: 题型:
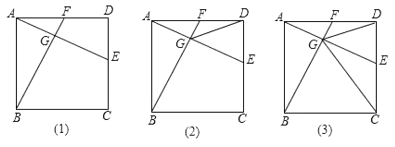
查看答案和解析>>【题目】如图(1)在正方形
 中,点
中,点 是
是 边上一动点,连接
边上一动点,连接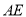 ,作
,作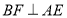 ,重足为
,重足为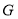 ,交
,交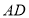 于
于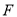 .
.(1)求证:
 ;
;(2)连接
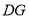 ,若
,若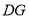 平分
平分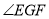 ,如图(2),求证:点
,如图(2),求证:点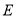 是
是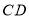 中点:
中点:(3)在(2)的条件下,连接
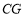 ,如图(3),求证:
,如图(3),求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A.
 B.
B. C.
C. D.
D.
相关试题

